2014-02-17
1532
Отклик зависимой переменной на единичное приращение независимой переменной (устойчивость моделей, содержащих авторегрессионые члены)
Рассмотрим отклик зависимой (эндогенной) переменной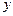 
на единичное приращение независимой (экзогенной) переменной 
.
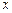Рассмотрим две модели:
;
.
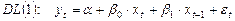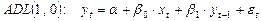Рассмотрим откликза один краткосрочный период (short-run), то есть мы не рассматриваем лаговые члены. Для первой модели имеем:
при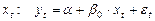 
,
при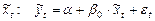 
,
где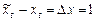 
— единичное приращение независимой переменной.
Тогда отклик зависимой переменной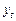 
имеет вид:
.
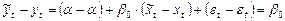Для второй модели отклик :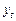
при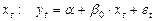 
,
при ,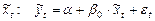
.
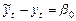То есть отклик зависимой переменной один и тот же.
Рассмотрим отклик зависимой переменной в долгосрочном периоде (long-run), то есть рассматриваем также и все лаговые переменные. Другими словами находим отклик зависимой переменной, которая является суммарным влиянием всех экзогенных переменных.
Для первой модели отклик равен:
,
,
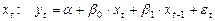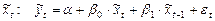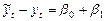
Для второй модели:
,
.
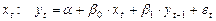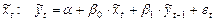В данном случае получить отклик по вышеуказанной схеме не удается. Поэтому преобразуем второе уравнение, чтобы избавиться от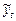 
в правой части
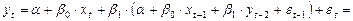
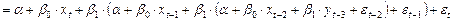
Отдельно выпишем члены, которые будут участвовать в отклике: константы сократятся и учитывать будем только члены, содержащие независимые переменные .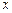
,
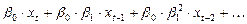тогда сам отклик будет формироваться следующим образом:
,
.
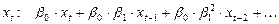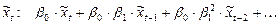В пределе отклик будет иметь вид:
.
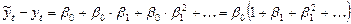Правая часть выражения — бесконечная геометрическая прогрессия. Сумма геометрической прогрессии может быть посчитана только тогда, когда прогрессия убывающая, то есть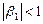 
. В таком случае, применив формулу суммы геометрической прогрессии, получим:
,
.
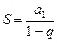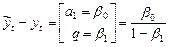Таким образом, для того чтобы отклик был конечным, необходимо, чтобы 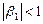. Это и есть условие устойчивости временного ряда.
То есть при исследовании отклика временного ряда необходимо в первую очередь обращать внимание на коэффициент перед первой лагированной объясняющей переменной. Если условие устойчивости выполняется (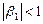), отклик будет конечным. В противном случае — бесконечным.
Понятие стационарности — более точное по сравнению с понятием устойчивости (но более трудно проверяемое). Стационарность различают двух видов:
- Строгая Стационарность (стационарность в узком смысле — strictly stationary SS);
- Слабая Стационарность (стационарность в широком смысле — weak stationary WS).
Определение SS: Ряд 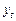строго стационарен, если совместное распределение 
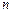наблюдений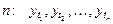 
не зависит от сдвига по времени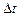 
, то есть совпадает с распределением
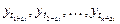для любых 
.
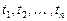На практике чаще используется понятие слабой стационарности или стационарности в широком смысле.
Определение WS: Ряд 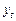слабо стационарен, если его среднее, дисперсия и ковариация не зависят от момента времени 
.
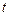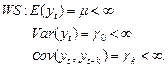
Ковариация зависит от лага, а не от момента времени.
Пример стационарного процесса — белый шум (white noise), помехи:
, 
~ 
.
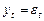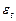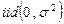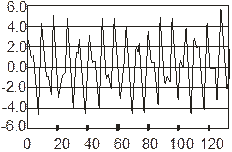
Рис.2 Белый Шум (White Noise)
Упражнение 1:
Показать, что white noise — стационарный ряд.
Упражнение 2:
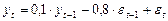
Является ли этот ряд стационарным? Ответ обоснуйте.
Примером нестационарного процесса является случайное блуждание (random walk).
