Таблица
Расчет χ2-критерия Пирсона
| i | xi = k | ni | 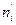
| 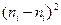
| 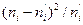
|
| 183,94 | 226,80 | 1,23 | |||
| 183,94 | 226,80 | 1,23 | |||
| 91,97 | 24,70 | 0,27 | |||
| 30,66 | 0,12 | 0,00 | |||
| 7,66 | 1,80 | 0,23 | |||
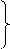 5 5
| 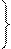 3 3
| 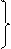 1,53 1,53
| |||
| 1 5 | 0,26 1,83 | 10,05 | 5,49 | ||
| 0,04 | |||||
| ∑ | – | 8,45 |
При расчете χ2 объединяем последние три интервала для того, чтобы в объединенных интервалах частота была не менее 5 (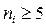 ).
).
Так как новое число интервалов (с учетом объединения трех последних) m = 6, а закон Пуассона определяется r = 1 параметром, то число степеней свободы 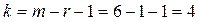 . По таблице χ2-распределения определяем
. По таблице χ2-распределения определяем 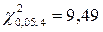 . Так как
. Так как 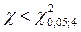 (8,45 < 9,49), то гипотеза H0 согласуется с опытными данными.
(8,45 < 9,49), то гипотеза H0 согласуется с опытными данными.
Пример 7.8. По данным примеров 7.4 и 7.6 на уровне значимости α=0,05 проверить гипотезу H0 о том, что случайная величина Х, распределена по нормальному закону.
Для определения статистики χ2 составим таблицу:
Таблица
Расчет χ2-критерия Пирсона
| № | Границы интервалов хi; хi+1 | Границы интервалов ui; ui+1 | ni | 
| 
| 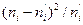
|
| -∞; 500 | -∞; -1,80 | 28,18 | 10,11 | 0,39 | ||
| 500; 1000 | -1,80; -0,91 | 113,85 | 1,32 | 0,01 | ||
| 1000; 1500 | -0,91; -0,03 | 240,15 | 8,12 | 0,03 | ||
| 1500; 2000 | -0,03; 0,86 | 248,21 | 7,78 | 0,03 | ||
| 2000; 2500 | 0,86; 1,74 | 120,58 | 6,66 | 0,06 | ||
| 2500; ∞ | 1,74; ∞ | 32,02 | 1,04 | 0,03 | ||
| ∑ | - | 782,99 | – | 0,55 |
Число интервалов m = 6, а нормальный закон определяется r = 2 параметрами, то число степеней свободы 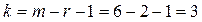 . По таблице χ2-распределения определяем
. По таблице χ2-распределения определяем 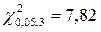 . Так как
. Так как 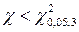 (0,55 < 7,82), то гипотеза H0 согласуется с опытными данными.
(0,55 < 7,82), то гипотеза H0 согласуется с опытными данными.
Проверим гипотезу о законе распределения также с помощью критерия Колмогорова. Для расчета значений функций распределения будем использовать следующую таблицу:
Таблица 8
| № | хi | ui | 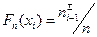
| 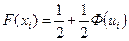
| 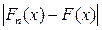
|
| -2,68 | 0,0037 | 0,0037 | |||
| -1,80 | 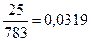
| 0,0360 | 0,0041 | ||
| -0,91 | 0,1788 | 0,1814 | 0,0026 | ||
| -0,03 | 0,4891 | 0,4880 | 0,0011 | ||
| 0,86 | 0,8097 | 0,8051 | 0,0046 | ||
| 1,74 | 0,9604 | 0,9591 | 0,0013 | ||
| 2,63 | 1,0000 | 0,9958 | 0,0042 | ||
| ∑ | – | – | – | 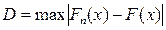 =
0,0046 =
0,0046
|
 .
.
Так как вычисленное значение λ не больше критического λα, определенного на уровне значимости α (λ0,05 =1,36), то нулевая гипотеза H0 не противоречит опытным данным.
 2014-02-17
2014-02-17 497
497








