2014-02-17
722
Вращение называется равномерным, если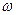 
= const.
; 
; 
; 
,
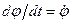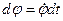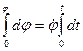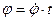Вращение будет равнопеременным, если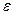 
= const. Алгебраическое угловое ускорение при этом тоже постоянно. Его при интегрировании можно вынести за знак интеграла. Имеем
; 
; 
; 
;
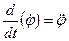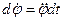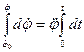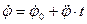Если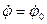 
при t = 0.
Так как
; ,
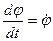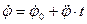То
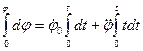
и
,
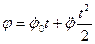Если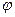 
= 0 при t = 0.
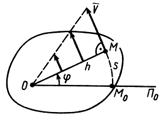Скорости и ускорения точек тела
Алгебраическую скорость точки М определяем по формуле
.
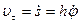Модуль скорости точки
.
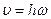Скорости точек тела при вращении вокруг неподвижной оси пропорциональны их кратчайшим расстояниям до этой оси (рис. 16). Коэффициентом пропорциональности является угловая скорость. Скорости точек направлены по касательным к траекториям и, следовательно, перпендикулярны радиусам вращения.
Ускорение точки разлагаем на касательную и нормальную составляющие, т. е.
.
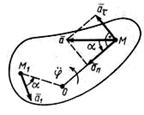
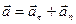Касательное и нормальное ускорения вычисляются по формулам
; 
,
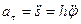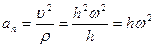так как для окружности радиус кривизны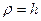 
(рис. 17). Таким образом,
, 
; 
.
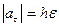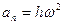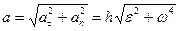Касательные, нормальные и полные ускорения точек, как и скорости, распределены тоже по линейному закону.
