Скорость и ускорение в сферических координатах

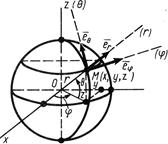
В качестве примера использования полученных формул вычислим скорость и ускорение точки в сферических координатах. Сферическими координатами точки М являются величины 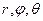(рис. 12). Координатной линией для r является прямая (r) c базисным вектором 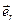. Координатной линией для 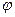служит параллель сферы с базисным вектором 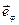и координатной линией 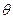- меридиан сферы с базисным вектором .

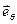Базисные векторы оказались ортогональными. Декартовы координаты x, y, z точки М через сферические выражаются следующими зависимостями:

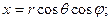
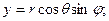
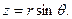
Вычисляя коэффициенты Ламэ, имеем:

;

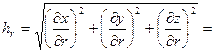
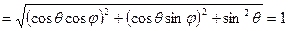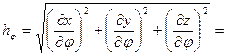
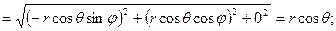
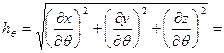
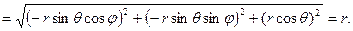
Проекции скорости на оси, направленные по базисным векторам, определяем по ранее полученной формуле 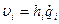(i=1,2,3). Получаем

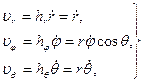
После этого

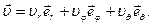
Для квадрата скорости и функции Т имеем

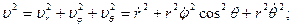
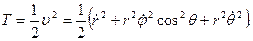
Проекции ускорения на оси, направленные по базисным векторам, вычисляются по формулам (8). Имеем

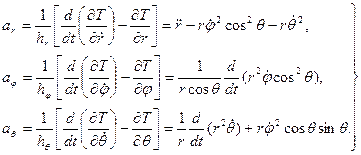
Для вектора ускорения получаем

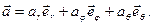
Модуль ускорения будет иметь следующее выражение:

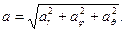
Аналогично можно вычислить ранее полученные скорость и ускорение точки в цилиндрических координатах.

ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА.