 Введем понятия векторов угловой скорости и углового ускорения тела. Если
Введем понятия векторов угловой скорости и углового ускорения тела. Если 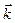 - единичный вектор оси вращения, направленный в ее положительную сторону, то векторы угловой скорости
- единичный вектор оси вращения, направленный в ее положительную сторону, то векторы угловой скорости 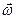 и углового ускорения
и углового ускорения 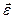 определяют выражениями
определяют выражениями
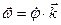 ;
; 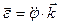 .
.
Так как 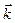 - постоянный по модулю и направлению вектор, то из вышеприведенных формул следует, что
- постоянный по модулю и направлению вектор, то из вышеприведенных формул следует, что

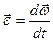 .
.
При 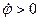 и
и 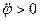 направления векторов
направления векторов 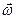 и
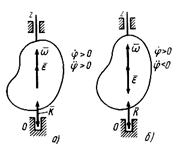
и 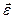 совпадают. Они оба направлены в положительную сторону оси вращения Oz (рис. 18,а). Если
совпадают. Они оба направлены в положительную сторону оси вращения Oz (рис. 18,а). Если 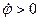 и
и 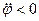 , то они направлены в противоположные стороны (рис. 18, б).
, то они направлены в противоположные стороны (рис. 18, б).
 Векторные формулы для скоростей и ускорений точек тела
Векторные формулы для скоростей и ускорений точек тела
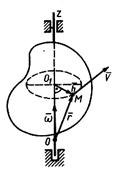
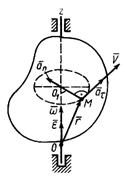
Выразим скорость, касательное, нормальное и полное ускорения точки тела в векторной форме (рис. 19).
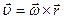 ,
,
Это выражение называется векторной формулой Эйлера.
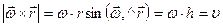 ,
,
так как 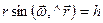 .
.
В частности, в качестве радиуса-вектора 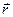 можно использовать вектор
можно использовать вектор 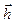 , направив его из точки О1 в точку М.
, направив его из точки О1 в точку М.
 Из определения ускорения и векторной формулы Эйлера имеем
Из определения ускорения и векторной формулы Эйлера имеем
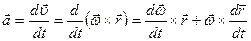 .
.
Учитывая, что
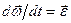 ;
; 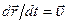 ,
,
получаем
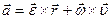 .
.
Первое слагаемое является касательным ускорением, а второе – нормальным, т. е.
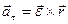 ;
;  .
.
В справедливости этой формулы убеждаемся вычислением их правых частей. Имеем (рис. 20)

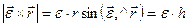 ,
,
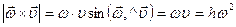
 2014-02-17
2014-02-17 1126
1126
