2014-02-09
4154
а) небольшой участок (кривизна земли не учитывается)
проекция – ортогональная
(проектируемые лучи параллельны и перпендикулярны к проектируемой поверхности).
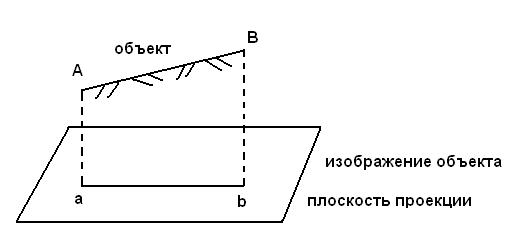
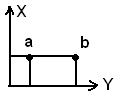
Для определения прямоугольных координат точки, нужно иметь прямоугольную систему координат.
Для определения высот точек, используем длины отвесных линий проектирования от точки Земли, до уровенной поверхности.
Начало отсчёта высот точек нуль пункт Кронштадского футштока (Балтийская система высот).
Численное значение высоты точки называется абсолютная высота точки или отметка точки
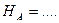
Разность высот двух точек называется превышением
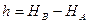
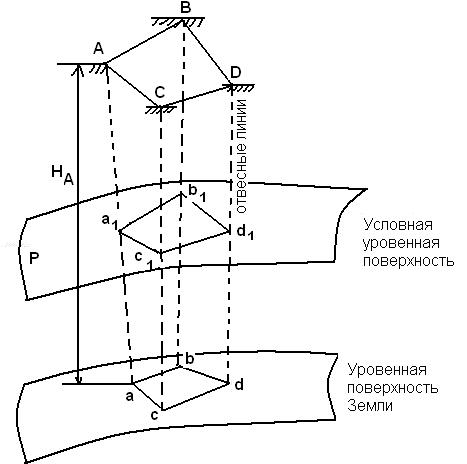
б) участок местности значительный (т.е. кривизна Земли должна учитываться).
Изображение значительных территорий.
Проектирование производится на уровенную поверхность Земли, по отношению к которой отвесные линии являются нормалями.
В геодезии при изображении значительных участков поверхности широкое распространение получена равноугольная поперечно-цилиндрическая проекция Гаусса.
Сущность этой проекции заключается в раздельном (зональном) проектировании земного эллипсоида на плоскость и установлении соответствия между геодезическими или координатами точки на поверхности земного эллипсоида и прямоугольными координатами этой же точки.
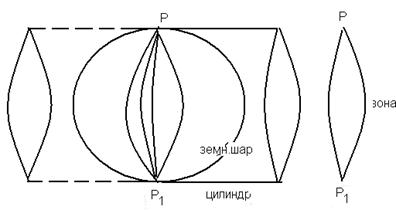
Проектирование поверхности:
- разделение поверхности на зоны меридианами с интервалом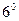 
(60 зон);
- последовательное проектирование зоны на поверхность цилиндра;
- развёртывание зон на плоскости.
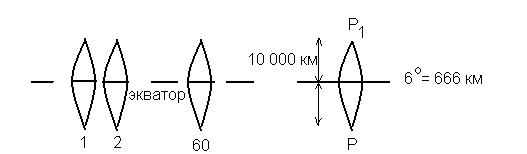
Изображение земной поверхности на плоскости
Для определения прямоугольных координат точек, установлена система координат.
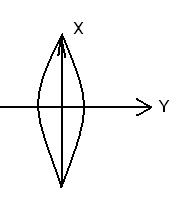
По оси Х масштаб без искажений
По оси Y масштаб по мере удаления точки от осевого меридиана будет меняться, т.е. при изображении линий и размеры будут содержать погрешность, но величина искажений не превышает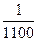 
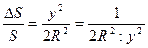
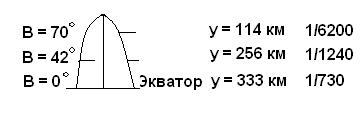
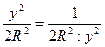
4.Кривизна Земли и её учёт в геодезии.
а) При измерении расстояний.
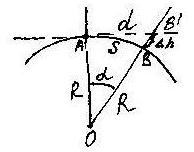
R- радиус Земли
α- центральный угол в радианной мере (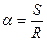
)
d- горизонтальное проложение
(кратчайшее расстояние по горизонтальной поверхности)
S- длина линии с учётом кривизны Земли.
Задача определить разность Δd длин d и S
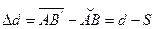
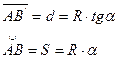
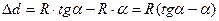
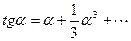
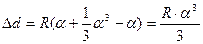т.к.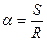
|
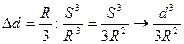
Анализ R=6371км.
S=10км.
Δd=1см.
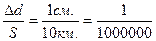
На участке земной поверхности при радиусе 10км., кривизну Земли можно не учитывать.
б) При измерении превышений (высот).
Задача определить Δh.
|
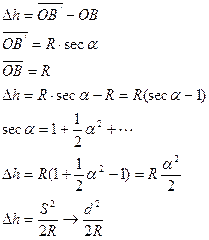
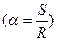
Анализ: R=6371км.
S=1км.
Δh=8см.
Допустимая разность Δh на 1км. не более 5см.
Уменьшим значение S до 0,3км. S=0,3км.
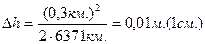
Кривизну Земли на участке длиной до 300 при измерении высот можно не учитывать.
Кривизна Земли не влияет на условие измерения (т.к. проекция равноугольная) и её при измерениях не учитывают.
