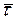 ,
, 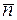 ,
, 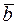 являются единичными векторами, направленными по трем взаимно перпендикулярным осям
являются единичными векторами, направленными по трем взаимно перпендикулярным осям 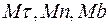 .
.
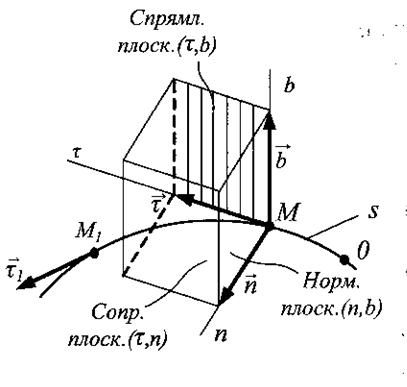
Рис.3
За время 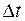 точка М по траектории перешла в положение
точка М по траектории перешла в положение 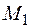 (рис. 4). За это время дуговая координата изменилась на
(рис. 4). За это время дуговая координата изменилась на 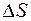 , а радиус-вектор — на
, а радиус-вектор — на 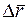 . Используя определение скорости, запишем:
. Используя определение скорости, запишем:
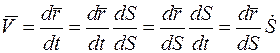 .
.
Обозначим
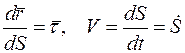 .
.
Вектор 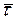 направлен по касательной к траектории, как производная вектора по скалярному аргументу (рис. 4), в сторону возрастания дуговой координаты
направлен по касательной к траектории, как производная вектора по скалярному аргументу (рис. 4), в сторону возрастания дуговой координаты 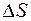 . Модуль этого вектора равен единице. Он представляет собой предел отношения длины хорды (
. Модуль этого вектора равен единице. Он представляет собой предел отношения длины хорды (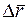 ) к длине стягивающей ее дуги (
) к длине стягивающей ее дуги (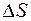 ) при стремлении
) при стремлении 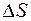 к нулю:
к нулю:
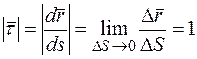 .
.
Скалярную величину 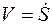 , представляющую проекцию вектора скорости на касательную, называют алгебраической ско
, представляющую проекцию вектора скорости на касательную, называют алгебраической ско ростью точки. Если
ростью точки. Если 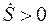 , то вектор скорости направлен по
, то вектор скорости направлен по 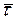 , т. е. в сторону возрастания значений S (рис. 11), а если
, т. е. в сторону возрастания значений S (рис. 11), а если 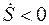 , то вектор скорости направлен в сторону убывающих значений дуговой координаты.
, то вектор скорости направлен в сторону убывающих значений дуговой координаты.
Тогда
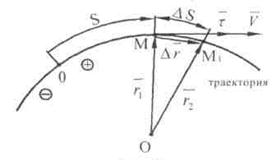
Рис. 4
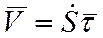 ,
,
или
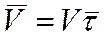 .
.
Для определения ускорения дифференцируем выражение по времени:
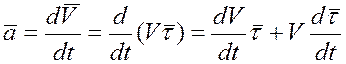 ,
,
где 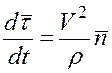 .
.
Тогда
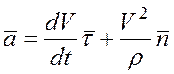 .
.
Ускорение точки состоит из двух взаимно перпендикулярных
составляющих. Одна 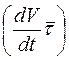 направлена по касательной к траектории, а другая
направлена по касательной к траектории, а другая 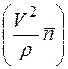 - по нормали к этой траектории в сторону ее вогнутости. Эти составляющие называют соответственно касательным и нормальным ускорениями точки. Они лежат в соприкасающейся плоскости.
- по нормали к этой траектории в сторону ее вогнутости. Эти составляющие называют соответственно касательным и нормальным ускорениями точки. Они лежат в соприкасающейся плоскости.
Проекция ускорения точки на бинормаль равна нулю, так как вектор ускорения расположен в соприкасающейся плоскости (рис. 5):
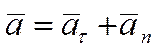 .
.
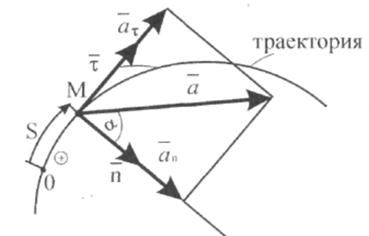
Рис. 5
Вектор касательного ускорения
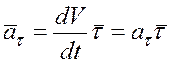 ,
,
модуль касательного ускорения
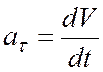 .
.
 Вектор нормального ускорения
Вектор нормального ускорения
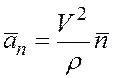 ,
,
модуль нормального ускорения
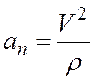 .
.
Модуль ускорения равен:
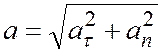 .
.
Угол отклонения вектора ускорения от нормали составит (рис. 5):
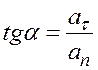 .
.
 2014-02-09
2014-02-09 502
502








