III. Оценки интеграла

Однородность

II. 3. Линейность

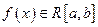и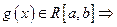

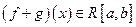
Формула:

,

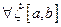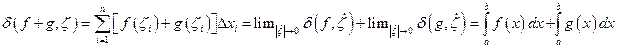
Свойство 3 может быть распространено

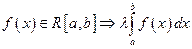
Доказательство:

Возьмем любое 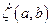, тогда:

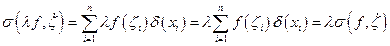
тогда:

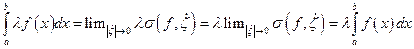
5. 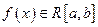и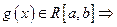

а.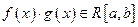

б.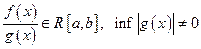

Свойство 5 может быть обобщено на конечное число интегральных функций.

6. 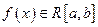и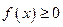

,

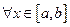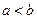
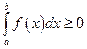
Для любого пунктирного разбиения 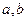составим интегральную сумму:

, (*)

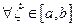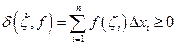т.к.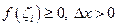

Используя свойства пределов, теорема о переходе предела к неравенству, при 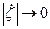перейдем в равенстве (*)

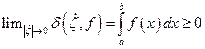
Из 6 следствие:

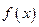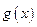
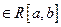и и ,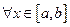

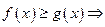
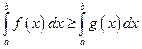
Доказательство следствия следует из 6, если обозначить:

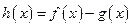и использовать свойства линейности определенного интеграла .

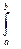7. Пусть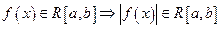

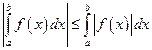
Доказательство:

Т.к. 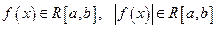, то применяя следствие из 6.

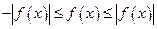
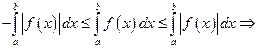
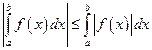ч.т.д.