Пример.
Имеются следующие исходные данные (таблица 2.1):
Таблица 2.1
| №№ | x1 | x2 | x3 | x4 | x5 | y |
| 0,8 | ||||||
| 5,3 | ||||||
| 4,7 | ||||||
| 3,3 | 0,5 | |||||
| 3,75 | 2,5 | |||||
| 3,2 | 1,5 | |||||
| Σ | 49,3 | 27,3 |
В таблице 2.1 приняты следующие обозначения:
x1- число членов семьи,
x2 - доход семьи,
x3 - число детей в семье,
x4 - среднедушевой доход,
x5 - затраты на питание,
y - расходы на покупку товаров длительного пользования. Y)Zq)rƒ)„ž) ¸)¹ǣ)ǤǨ)ǩǮ)ǯǰ'DZ
Построим два уравнения линейной регрессии:
1) Уравнение парной линейной регрессии y = a0 + a1 x4 (выражающее зависимость расходов на покупку товаров длительного пользования от среднедушевого дохода семьи);
2) Уравнение двухфакторной линейной регрессии y = a0 + a1 x2 + a2 x4 (выражающее зависимость расходов на покупку товаров длительного пользования от дохода семьи и среднедушевого дохода)
Для построения первого уравнения необходимо построить вспомогательную таблицу (см. таблицу 2.2.), чтобы на основе итоговых сумм в нижней строке этой таблицы рассчитать параметры уравнения линейной регрессии по формулам, известным из курса теории статистики (изученного в третьем семестре).
Таблица 2.2
Вспомогательная таблица для расчета параметров
| x4 | y | x42 | x*y |
| 5,0 | 1,0 | 25,0 | 5,0 |
| 6,0 | 5,0 | 36,0 | 30,0 |
| 9,0 | 6,0 | 81,0 | 54,0 |
| 3,0 | 0,8 | 9,0 | 2,4 |
| 5,3 | 3,0 | 28,4 | 16,0 |
| 4,7 | 3,0 | 21,8 | 14,0 |
| 6,0 | 4,0 | 36,0 | 24,0 |
| 3,3 | 0,5 | 11,1 | 1,7 |
| 3,8 | 2,5 | 14,1 | 9,4 |
| 3,2 | 1,5 | 10,2 | 4,8 |
| 49,28 | 27,30 | 272,64 | 161,24 |
Подсчитав суммы в нижней строке таблицы, находим параметры уравнения парной линейной регрессии по формулам:
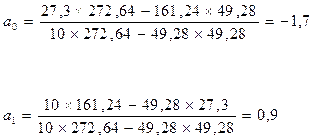
Таким образом, окончательный вид уравнения регрессии:
y = -1,7 + 0,9 x4.
Теперь построим вспомогательную таблицу, чтобы рассчитать ошибку аппроксимации и индекс детерминации для данного уравнения.
Как известно из курса теории статистики, ошибка аппроксимации находится по формуле:
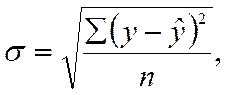
Где y – исходные (фактические) значения исходного ряда данных, а 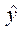 - расчетные значения (т.е. рассчитанные на основе построенного уравнения регрессии).
- расчетные значения (т.е. рассчитанные на основе построенного уравнения регрессии).
А индекс детерминации – по формуле:
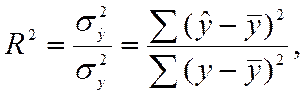
Где 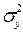 - дисперсия фактических значений признака,
- дисперсия фактических значений признака, 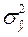 - дисперсия расчетных значений, y – исходные (фактические) значения исходного ряда данных,
- дисперсия расчетных значений, y – исходные (фактические) значения исходного ряда данных, 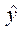 - расчетные значения, а
- расчетные значения, а 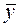 – среднее значение (одинаковое для расчетных и фактических значений). В таблице 2.3. выполнены вспомогательные расчеты для определения этих показателей.
– среднее значение (одинаковое для расчетных и фактических значений). В таблице 2.3. выполнены вспомогательные расчеты для определения этих показателей.
Таблица 2.3
Вспомогательная таблица для расчета ошибки аппроксимации и индекса детерминации (для уравнения 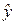 = -1,7+0,9x4)
= -1,7+0,9x4)
Фактические значения (y)
и расчетные значения (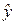 ) )
| Расчет ошибки аппроксимации (σ) | Расчет дисперсии фактических значений
(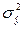 ) )
| Расчет дисперсии расчетных значений (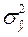 ) )
| |||
| Y | 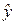 = -1,7+0,9x4 = -1,7+0,9x4
| (y - 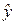 )2 )2
| 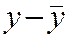
| 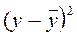
| 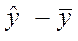
| 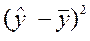
|
| 1,0 | 2,79 | 3,22 | -1,73 | 2,99 | 0,06 | 0,004 |
| 5,0 | 3,69 | 1,71 | 2,27 | 5,15 | 0,96 | 0,925 |
| 6,0 | 6,38 | 0,15 | 3,27 | 10,69 | 3,65 | 13,351 |
| 0,8 | 1,00 | 0,04 | -1,93 | 3,72 | -1,73 | 2,994 |
| 3,0 | 3,09 | 0,01 | 0,27 | 0,07 | 0,36 | 0,132 |
| 3,0 | 2,50 | 0,25 | 0,27 | 0,07 | -0,23 | 0,055 |
| 4,0 | 3,69 | 0,10 | 1,27 | 1,61 | 0,96 | 0,925 |
| 0,5 | 1,30 | 0,64 | -2,23 | 4,97 | -1,43 | 2,049 |
| 2,5 | 1,67 | 0,68 | -0,23 | 0,05 | -1,06 | 1,118 |
| 1,5 | 1,18 | 0,10 | -1,23 | 1,51 | -1,55 | 2,406 |
| 27,30 | 27,30 | 6,90 | 0,00 | 30,86 | 0,00 | 23,96 |
Подсчитав суммы в нижней строке таблицы, легко вычислить все необходимые величины. Так как сумма фактических значений y равна сумме расчетных значений, то и среднее значение y совпадает со средним значением yx и равно: 27,3/10= 2,7
Ошибка аппроксимации: s = 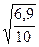 = 0,831
= 0,831
Дисперсия фактических значений (y): sy2 = 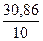 = 3,09
= 3,09
Дисперсия расчетных значений (yx): syx2 = 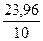 = 2,40
= 2,40
Индекс детерминации: R2 = 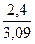 = 0,777
= 0,777
Теперь найдем параметры уравнения двухфакторной линейной регрессии y = a0 + a1 x2 + a2 x4, включив в уравнение регрессии, кроме фактора x4 дополнительно фактор x2.
Так же, как для предыдущего уравнения построим вспомогательную таблицу, чтобы решить затем систему нормальных уравнений и найти параметры уравнения регрессии.
Таблица 2.4.
Вспомогательная таблица для расчета параметров уравнения регрессии y = a0 + a1 x2 + a2 x4
| Y | x2 | x4 | x22 | x42 | x2*x4 | x2*y | x4*y |
| 0,8 | 4,8 | ||||||
| 12,6 | 158,76 | 176,4 | 37,8 | ||||
| 0,5 | 6,5 | ||||||
| 2,5 | 37,5 | 37,5 | |||||
| 1,5 | 22,5 | ||||||
| 27,3 | 138,6 | 1954,76 | 1830,4 | 406,3 | 395,3 |
На основе сумм, рассчитанных в нижней строке этой таблицы, построим систему нормальных уравнений:
10a0+130a1+138,6a2=27,3
130a0+1886a1+1830,4a2=406,3
10a0+1830,4a1+1954,76a2=18,3
 2014-02-17
2014-02-17 531
531








