Каноническое уравнение этой поверхности:
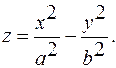 (31)
(31)
Из уравнения следует, что плоскости 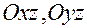 являются плоскостями симметрии, ось
являются плоскостями симметрии, ось 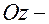 ось гиперболического параболоида.
ось гиперболического параболоида.
1) Линии пересечения гиперболического параболоида плоскостями 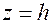
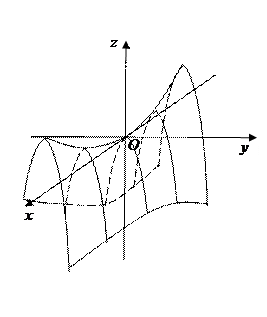 представляют собой при
представляют собой при 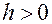 гиперболы
гиперболы 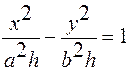 с полуосями
с полуосями 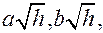 а при
а при 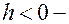 сопряженные для них гиперболы
сопряженные для них гиперболы 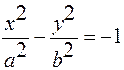 с полуосями
с полуосями 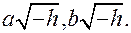
Сечение плоскостью 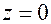 пересекает поверхность по двум прямым
пересекает поверхность по двум прямым
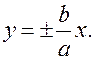
2) 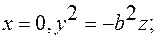 парабола в плоскости
парабола в плоскости 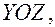
3) 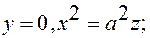
Можно убедиться в том, что гиперболический параболоид может быть получен путем параллельного перемещения параболы, представляющей собой сечение плоскостью 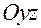 , когда её вершина движется вдоль параболы, являющейся сечением параболоида плоскостью
, когда её вершина движется вдоль параболы, являющейся сечением параболоида плоскостью
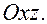
 2014-02-09
2014-02-09 1784
1784







