Если в функции 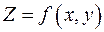 аргументы
аргументы 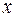 и
и 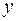 в свою очередь являются функциями аргумента
в свою очередь являются функциями аргумента 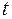 , то по отношению к переменной
, то по отношению к переменной 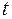 функцию
функцию 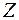 называют сложной. Производная такой функции находится по правилу
называют сложной. Производная такой функции находится по правилу
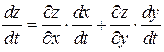 .
.
В функции 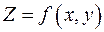 аргументы могут быть также функциями двух переменных
аргументы могут быть также функциями двух переменных 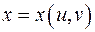 и
и 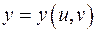 . По отношению к переменным
. По отношению к переменным 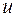 и
и 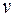 функцию
функцию 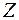 опять же называют сложной. Частные производные такой сложной функции находятся по правилам аналогичным доказанному выше
опять же называют сложной. Частные производные такой сложной функции находятся по правилам аналогичным доказанному выше
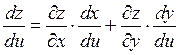 ,
,
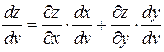 .
.
Пример 5.1.
Найти частную производную 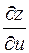 функции
функции 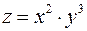 , если
, если 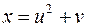 ,
, 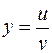 .
.
Применяя известное правило, запишем
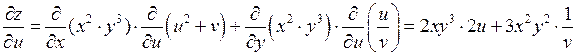 .
.
При неявном задании функции одной переменной ее определяют из уравнения 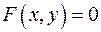 .
.
Не разрешая данное уравнение относительно 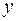 , производную данной функции можно определить по правилу
, производную данной функции можно определить по правилу
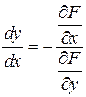
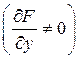 .
.
Уравнение 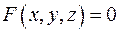 неявно определяет функцию двух переменных
неявно определяет функцию двух переменных 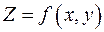 . Ее частные производные находятся по аналогичным формулам:
. Ее частные производные находятся по аналогичным формулам:
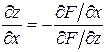 ,
, 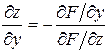 .
.
Пример 5.2.
Найти 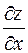 функции, заданной неявно уравнением
функции, заданной неявно уравнением 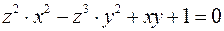 .
.
По правилу, указанному выше, имеем
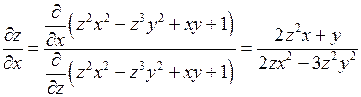 .
.
 2014-02-09
2014-02-09 564
564








