Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0(х0, у0) верно неравенство
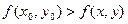
то точка М0 называется точкой максимума.
Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0(х0, у0) верно неравенство
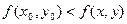
то точка М0 называется точкой минимума.
Теорема. (Необходимые условия экстремума).
Если функция f(x,y) в точке (х0, у0) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю 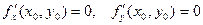 , либо хотя бы одна из них не существует.
, либо хотя бы одна из них не существует.
Эту точку (х0, у0) будем называть критической точкой.
Теорема. (Достаточные условия экстремума).
Пусть в окрестности критической точки (х0, у0) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:
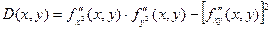
1) Если D(x0, y0) > 0, то в точке (х0, у0) функция f(x, y) имеет экстремум, если
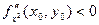 - максимум, если
- максимум, если 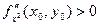 - минимум.
- минимум.
2) Если D(x0, y0) < 0, то в точке (х0, у0) функция f(x, y) не имеет экстремума
В случае, если D = 0, вывод о наличии экстремума сделать нельзя.
Пример 6.1. Исследовать функцию 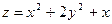 на экстремум.
на экстремум.
Находим частные производные первого порядка и приравниваем их к нулю:
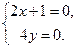
Стационарная точка данной функции имеет координаты 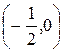 .
.
Вычислим вторые производные 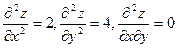 .
.
Следовательно, 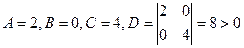 .
.
Экстремум имеется, т.к. 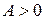 , то в точке
, то в точке 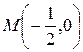 - минимум,
- минимум, 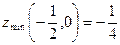 .
.
Пример 6.2. Исследовать функцию  на экстремум.
на экстремум.
Находим частные производные и приравниваем их к нулю
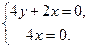
Стационарная точка данной функции имеет координаты 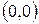 .
.
Вычислим вторые производные: 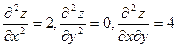 .
.
Следовательно, 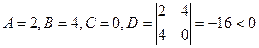 .
.
Экстремум отсутствует, т.к. 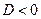 .
.
 2014-02-09
2014-02-09 488
488








