Тип 6.Уравнение в полных дифференциалах

Если уравнение записано в виде

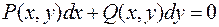, (1)

и выполняется соотношение 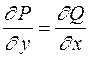, тогда правая часть уравнения является полным дифференциалом некоторой функции 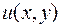и его можно переписать в виде 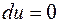. Отсюда следует, что

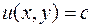. (2)

Выражение (2) является общим решением дифференциального уравнения (1), которое в этом случае называют уравнением в полных дифференциалах. Таким образом, интегрирование данного вида уравнений сводится к задаче отыскания функции 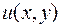по ее полному дифференциалу.

Алгоритм решения:

1. Проверить выполнимость условия

2. Решить систему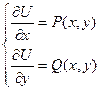

3. Записать ответ U(x,y)=0.

Пример. 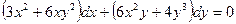- уравнение в полных дифференциалах.