Уравнение 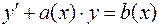 , линейное относительно неизвестной функции у и ее производной
, линейное относительно неизвестной функции у и ее производной 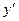 , называется неоднородным линейным дифференциальным уравнением первого порядка. Функции a(x), b(x) должны быть непрерывны в некоторой области.
, называется неоднородным линейным дифференциальным уравнением первого порядка. Функции a(x), b(x) должны быть непрерывны в некоторой области.
Если b(x) = 0. то уравнение называют однородным линейным дифференциальным уравнением.
Общее решение линейного дифференциального уравнения всегда можно записать в виде:
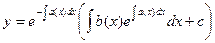 , где с – произвольная постоянная.
, где с – произвольная постоянная.
Полезно иметь в виду, что иногда дифференциальное уравнение является линейным относительно х как функции у, т.е. может быть приведено к виду 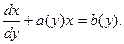
Его общее решение находится по формуле:
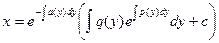 , где с – произвольная постоянная.
, где с – произвольная постоянная.
Алгоритм решения:
1 способ.
Найти решение дифференциального уравнения по формуле 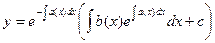 .
.
2 способ.
Ввести 2 неизвестные функции u(x) и v(x) по формуле y=u(x)v(x) (подстановка Бернулли). Тогда 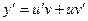 . Подставив выражение для y и
. Подставив выражение для y и 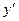 в уравнение получим уравнение
в уравнение получим уравнение 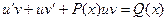 , которое преобразуется к виду
, которое преобразуется к виду 
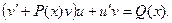 Пользуясь тем, что одна из неизвестных функций, например
Пользуясь тем, что одна из неизвестных функций, например 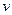 , может быть выбрана достаточно произвольно (так как только произведение
, может быть выбрана достаточно произвольно (так как только произведение 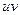 должно удовлетворять исходному уравнению), составляем систему:
должно удовлетворять исходному уравнению), составляем систему: 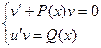 . Из первого уравнения (уравнение с разделяющимися переменными) находим v=v(x), затем из второго уравнения находим u=u(x,C). Затем находим общее решение уравнения y= v(x)◦ u(x,C).
. Из первого уравнения (уравнение с разделяющимися переменными) находим v=v(x), затем из второго уравнения находим u=u(x,C). Затем находим общее решение уравнения y= v(x)◦ u(x,C).
Примеры.
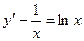 - линейное дифференциальное уравнение (линейное относительно y).
- линейное дифференциальное уравнение (линейное относительно y).
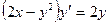 - линейное дифференциальное уравнение (линейное относительно х).
- линейное дифференциальное уравнение (линейное относительно х).
 2014-02-09
2014-02-09 612
612








