Лекция 4
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной. Линейное уравнение имеет вид
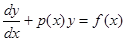 , (1)
, (1)
или, в другой записи,
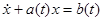 , (2)
, (2)
где 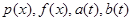 в дальнейшем будем считать непрерывными функциями
в дальнейшем будем считать непрерывными функциями  либо
либо  в той области, в которой требуется проинтегрировать уравнения (1) либо (2).
в той области, в которой требуется проинтегрировать уравнения (1) либо (2).
Если 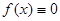 , то уравнение (1) называется линейным однородным. В линейном однородном уравнении переменные разделяются:
, то уравнение (1) называется линейным однородным. В линейном однородном уравнении переменные разделяются:
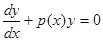 , откуда
, откуда 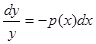 ,
,
и, интегрируя, получаем
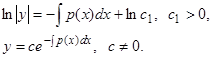 (3)
(3)
При делении на 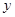 мы потеряли решение
мы потеряли решение 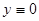 , однако оно может быть включено в найденное семейство решений (3), если считать, что
, однако оно может быть включено в найденное семейство решений (3), если считать, что 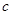 может принимать и значение 0.
может принимать и значение 0.
Для интегрирования неоднородных уравнений (1), (2) известно несколько методов.
Метод интегрирующего множителя. Рассмотрим его применительно к уравнению (2).
Умножим обе части уравнения (2) на функцию 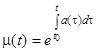 — интегрирующий множитель. Здесь
— интегрирующий множитель. Здесь 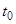 — произвольная точка из области непрерывности
— произвольная точка из области непрерывности 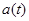 . Полученное уравнение запишем в виде
. Полученное уравнение запишем в виде
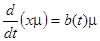 .
.
Интегрируя в пределах от 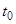 до
до 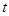 , получим
, получим
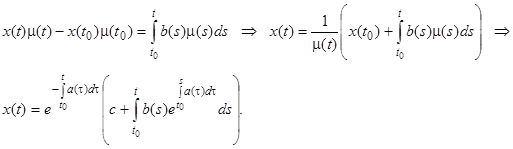
Пример. 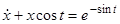 .
.
Находим интегрирующий множитель 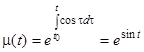 (здесь выбрано
(здесь выбрано 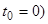 . Умножая левую и правую части данного уравнения на
. Умножая левую и правую части данного уравнения на 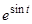 , получим
, получим
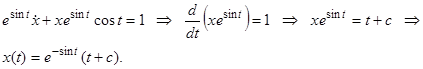
Также для интегрирования линейного неоднородного уравнения (1) либо (2) может быть применен так называемый метод вариации произвольной постоянной. Рассмотрим его для уравнения (1). При применении этого метода сначала интегрируется соответствующее (т.е. имеющее ту же левую часть) однородное уравнение 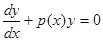 , общее решение которого, как мы уже знаем, имеет вид
, общее решение которого, как мы уже знаем, имеет вид 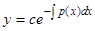 . При постоянном
. При постоянном 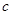 функция
функция 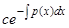 является решением однородного уравнения. Попробуем теперь удовлетворить неоднородному уравнению, считая
является решением однородного уравнения. Попробуем теперь удовлетворить неоднородному уравнению, считая 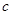 функцией от
функцией от  , т.е. по существу совершая замену переменных
, т.е. по существу совершая замену переменных 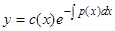 , где
, где 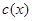 — новая неизвестная функция от
— новая неизвестная функция от  .
.
Вычисляя производную
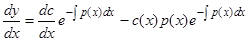
и подставляя в исходное уравнение (1), получим
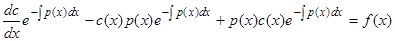
или 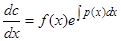 , откуда, интегрируя, находим
, откуда, интегрируя, находим
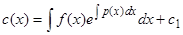 ,
,
а следовательно,
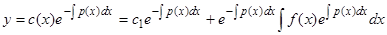 . (4)
. (4)
Итак, общее решение неоднородного линейного уравнения равно сумме общего решения соответствующего однородного уравнения 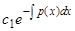 и частного решения неоднородного уравнения
и частного решения неоднородного уравнения 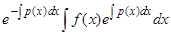 , получающегося из (4) при
, получающегося из (4) при 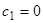 .
.
Заметим, что в конкретных примерах нецелесообразно пользоваться громоздкой и трудно запоминаемой формулой (4), значительно легче каждый раз повторять все приведенные выше вычисления.
Пример. 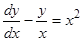 .
.
Интегрируем соответствующее однородное уравнение
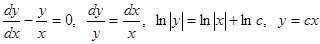 .
.
Считаем теперь 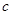 функцией от
функцией от  , тогда
, тогда 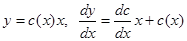 и, подставляя в исходное уравнение, после упрощения получаем
и, подставляя в исходное уравнение, после упрощения получаем
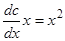 или
или 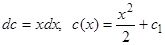 .
.
Следовательно, общее решение неоднородного уравнения 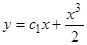 .
.
Пример. 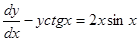 .
.
Интегрируем соответствующее однородное уравнение
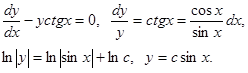
Варьируем постоянную 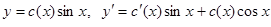 .
.
Подставляя в исходное уравнение, получим
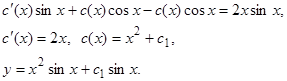
Пример. 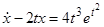 .
.
Однородное уравнение имеет вид 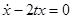 . Функция
. Функция 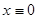 является решением однородного уравнения. Остальные его решения найдем, разделяя переменные:
является решением однородного уравнения. Остальные его решения найдем, разделяя переменные:
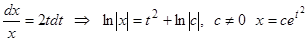 .
.
Решение 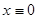 можно получить из последнего соотношения при
можно получить из последнего соотношения при 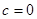 . Поэтому общее решение однородного уравнения дается формулой
. Поэтому общее решение однородного уравнения дается формулой 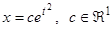 . Решение неоднородного уравнения ищем в виде
. Решение неоднородного уравнения ищем в виде 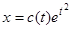 . Подставив это в исходное неоднородное уравнение, получим
. Подставив это в исходное неоднородное уравнение, получим
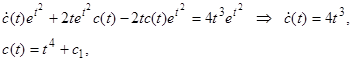
где 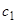 — произвольная постоянная. Подставляя найденную функцию
— произвольная постоянная. Подставляя найденную функцию 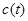 в вид решения неоднородного уравнения (
в вид решения неоднородного уравнения (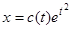 ), получаем общее решение исходного уравнения:
), получаем общее решение исходного уравнения: 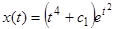 .
.
Пример. В электрической цепи с самоиндукцией происходит процесс установления переменного тока. Напряжение 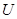 является заданной функцией времени
является заданной функцией времени 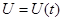 , сопротивление
, сопротивление 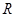 и самоиндукция
и самоиндукция 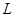 постоянны, начальная сила тока
постоянны, начальная сила тока 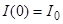 задана. Найти зависимость силы тока
задана. Найти зависимость силы тока 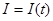 от времени.
от времени.
Пользуясь законом Ома для цепи с самоиндукцией, получим
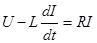 .
.
Решение этого линейного уравнения, удовлетворяющее начальному условию 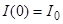 , согласно (4), имеет вид
, согласно (4), имеет вид
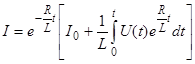 . (5)
. (5)
При постоянном напряжении 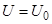 получим
получим 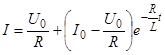 .
.
Интересен случай синусоидального переменного напряжения 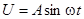 . При этом, согласно (5), получим
. При этом, согласно (5), получим 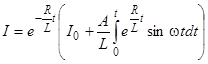 . Стоящий в правой части интеграл легко вычисляется.
. Стоящий в правой части интеграл легко вычисляется.
Некоторые уравнения становятся линейными, если 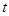 считать функцией, а
считать функцией, а  — аргументом. Так, нелинейное уравнение
— аргументом. Так, нелинейное уравнение 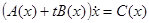 становится линейным, если
становится линейным, если 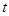 считать функцией от
считать функцией от  :
:
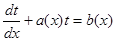 ,
,
где 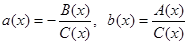 .
.
Пример. Решить уравнение 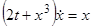 .
.
Запишем это уравнение в виде
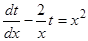 .
.
Последнее уравнение является линейным и решается аналогично рассмотренным ранее.
Многие дифференциальные уравнения путем замены переменных могут быть сведены к линейным. Например, уравнение Бернулли, имеющее вид
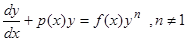 ,
,
или 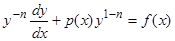 , (6)
, (6)
заменой переменных 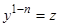 сводится к линейному уравнению Действительно, дифференцируя
сводится к линейному уравнению Действительно, дифференцируя 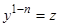 , находим
, находим 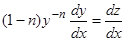 и, подставляя в (6), получим линейное уравнение
и, подставляя в (6), получим линейное уравнение 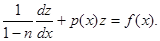
Пример. 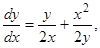
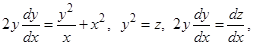
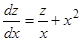 , и далее — как в первом примере.
, и далее — как в первом примере.
Можно также записать уравнение Бернулли в таком виде:
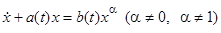 .
.
Чтобы привести его к линейному, разделим обе его части на 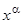 и сделаем замену
и сделаем замену 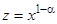 . Тогда имеем:
. Тогда имеем:
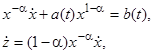
тогда 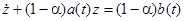 .
.
Последнее уравнение является линейным.
Пример. 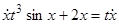 .
.
Запишем это уравнение в виде 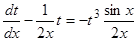 . Полученное уравнение является уравнением Бернулли. Сделав в нем замену
. Полученное уравнение является уравнением Бернулли. Сделав в нем замену 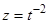 , получим линейное уравнение
, получим линейное уравнение
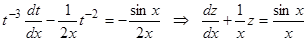 .
.
Интегрирующий множитель этого уравнения имеет вид 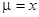 . Умножив на
. Умножив на 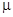 это уравнение, получим
это уравнение, получим
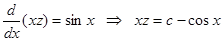 .
.
Таким образом, 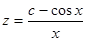 , или
, или 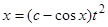 .
.
Уравнение 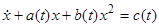 называется уравнением Риккати. Это уравнение в общем виде не решается в квадратурах. Однако, если известно одно частное его решение
называется уравнением Риккати. Это уравнение в общем виде не решается в квадратурах. Однако, если известно одно частное его решение 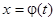 , то заменой
, то заменой 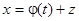 уравнение Риккати сводится к уравнению Бернулли. Действительно, подставив
уравнение Риккати сводится к уравнению Бернулли. Действительно, подставив 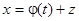 в уравнение Риккати, получим
в уравнение Риккати, получим
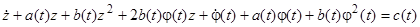 ,
,
тогда 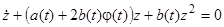 . Это уравнение является уравнением Бернулли.
. Это уравнение является уравнением Бернулли.
Пример. 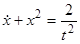 . Это уравнение является уравнением Риккати. Нетрудно заметить, что
. Это уравнение является уравнением Риккати. Нетрудно заметить, что 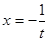 является его решением. Замена
является его решением. Замена 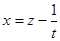 приводит исходное уравнение к виду
приводит исходное уравнение к виду 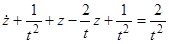 , тогда
, тогда
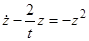 .
.
Последнее уравнение является уравнением Бернулли. Оно имеет очевидное решение 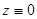 . Замена
. Замена 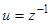 приводит уравнение Бернулли к уравнению
приводит уравнение Бернулли к уравнению
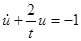 ,
,
которое является линейным. Его интегрирующий множитель имеет вид 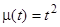 . Умножив на
. Умножив на 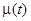 обе части последнего уравнения, получим
обе части последнего уравнения, получим 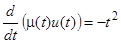 , или
, или 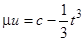 , и отсюда
, и отсюда 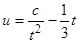 , или
, или 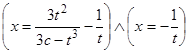 .
.
Перепишем в других обозначениях. Уравнение 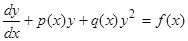 , (уравнение Риккати), в общем виде не интегрируется в квадратурах, но может быть заменой переменных преобразовано в уравнение Бернулли, если известно одно частное решение
, (уравнение Риккати), в общем виде не интегрируется в квадратурах, но может быть заменой переменных преобразовано в уравнение Бернулли, если известно одно частное решение 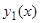 этого уравнения. Действительно, полагая
этого уравнения. Действительно, полагая 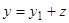 , получим
, получим
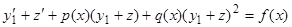
или, так как 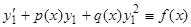 , будем иметь уравнение Бернулли
, будем иметь уравнение Бернулли
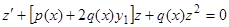 .
.
Пример. 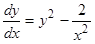 .
.
В этом примере нетрудно подобрать частное решение 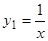 . Полагая
. Полагая 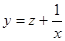 , получим
, получим 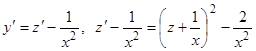 , или
, или
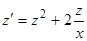 — уравнение Бернулли.
— уравнение Бернулли.
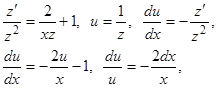
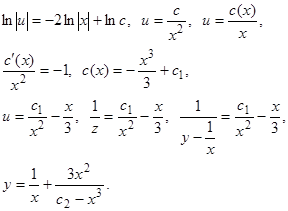
 2014-02-17
2014-02-17 1798
1798
