ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Лекция 7
Будем по-прежнему обозначать независимую переменную через 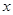 , а искомую функцию через
, а искомую функцию через 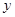 . Дифференциальное уравнение
. Дифференциальное уравнение 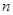 -го порядка (
-го порядка (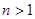 ) имеет вид
) имеет вид
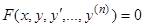 , (1)
, (1)
где 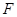 есть непрерывная функция всех своих аргументов, при этом левая часть, во всяком случае, зависит от старшей производной
есть непрерывная функция всех своих аргументов, при этом левая часть, во всяком случае, зависит от старшей производной 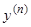 . Вблизи начальных значений
. Вблизи начальных значений 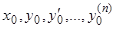 , удовлетворяющих условиям
, удовлетворяющих условиям
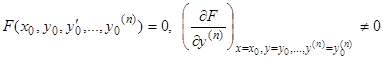 ,
,
мы можем, по теореме о существовании неявной функции, разрешить уравнение (1) относительно 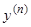 и представить его в виде
и представить его в виде
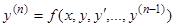 . (1.1)
. (1.1)
Можно доказать существование и единственность (при некоторых условиях) решения уравнения (1.1), определяемого начальными условиями: при 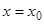 имеем
имеем
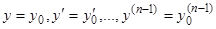 , (2)
, (2)
где 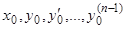 — заданные числа. Эта задача также, как и в случае уравнений первого порядка, называется задачей Коши, или задачей с начальными значениями.
— заданные числа. Эта задача также, как и в случае уравнений первого порядка, называется задачей Коши, или задачей с начальными значениями.
Теорема существования и единственности решения. Существует единственное решение дифференциального уравнения 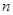 -го порядка
-го порядка 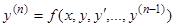 , удовлетворяющее условиям
, удовлетворяющее условиям 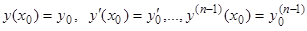 , если в окрестности начальных значений
, если в окрестности начальных значений 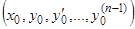 функция
функция 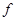 является непрерывной функцией всех своих аргументов и удовлетворяет условию Липшица по всем аргументам, начиная со второго.
является непрерывной функцией всех своих аргументов и удовлетворяет условию Липшица по всем аргументам, начиная со второго.
|
|
|
Последнее условие может быть заменено более грубым условием существования в той же окрестности ограниченных частных производных первого порядка от функции 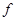 по всем аргументам, начиная со второго.
по всем аргументам, начиная со второго.
Общим решением дифференциального уравнения 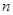 -го порядка называется множество решений, состоящее из всех без исключения частных решений. Общее решение уравнения (1.1) имеет вид
-го порядка называется множество решений, состоящее из всех без исключения частных решений. Общее решение уравнения (1.1) имеет вид
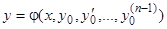 . (3)
. (3)
Замечая, что начальные значения 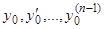 являются параметрами, т.е. произвольными постоянными, приходим к следующему выводу: общее решение дифференциального уравнения
являются параметрами, т.е. произвольными постоянными, приходим к следующему выводу: общее решение дифференциального уравнения 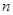 -го порядка содержит
-го порядка содержит 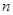 произвольных постоянных и имеет вид
произвольных постоянных и имеет вид
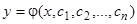 . (3.1)
. (3.1)
Если соотношение, связывающее 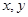 и
и 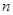 произвольных постоянных, дано в виде, не разрешенном относительно
произвольных постоянных, дано в виде, не разрешенном относительно 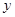 :
:
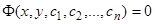 , (4)
, (4)
то мы будем называть такое соотношение общим интегралом уравнения (1) или (1.1).
Покажем, как решить задачу Коши, если известно общее решение (3.1). Из соотношения (3.1) и тех, которые получаются из него дифференцированием по 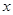 , подставляя в них вместо
, подставляя в них вместо 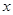 начальное значение
начальное значение 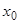 , а вместо
, а вместо 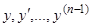 их начальные значения, получим равенства
их начальные значения, получим равенства
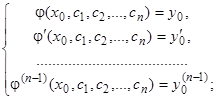 (5)
(5)
рассматривая равенства (5) как 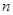 уравнений с
уравнений с 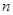 неизвестными,
неизвестными, 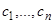 , мы получим, вообще говоря, числовые значения
, мы получим, вообще говоря, числовые значения 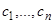 , соответствующие тому частному решению, которое отвечает данным начальным условиям (2). Точно так же, если дан общий интеграл (4), то, подставляя в него вместо
, соответствующие тому частному решению, которое отвечает данным начальным условиям (2). Точно так же, если дан общий интеграл (4), то, подставляя в него вместо 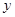 решение (3.1) уравнения (1), полученное разрешением уравнения (4) относительно
решение (3.1) уравнения (1), полученное разрешением уравнения (4) относительно 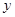 , мы получим тождество; дифференцируем его по
, мы получим тождество; дифференцируем его по 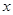 , помня, что
, помня, что 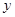 является функцией
является функцией 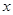 , и подставляем в полученные равенства начальные значения (2). Получаем
, и подставляем в полученные равенства начальные значения (2). Получаем
|
|
|
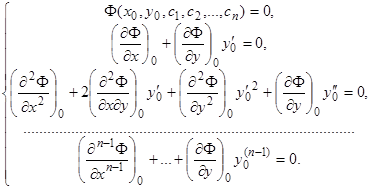 (5.1)
(5.1)
Символ 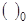 указывает, что в данном выражении вместо
указывает, что в данном выражении вместо 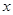 и
и 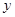 следует подставить
следует подставить 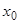 и
и 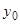 . Мы опять получаем
. Мы опять получаем 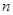 уравнений для определения
уравнений для определения 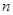 неизвестных,
неизвестных, 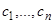 , т.е. мы и в этом случае можем, вообще говоря, решить задачу Коши.
, т.е. мы и в этом случае можем, вообще говоря, решить задачу Коши.
Теперь установим некоторые случаи, когда уравнение (1) или (1.1) может быть проинтегрировано до конца в квадратурах или, по крайней мере, когда задача его интегрирования может быть сведена к интегрированию дифференциального уравнения порядка меньшего, чем 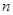 .
.
 2014-02-17
2014-02-17 890
890








