2014-02-17
4278
Лекция 6
Ранее мы доказали теорему существования и единственности решения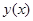 
уравнения 
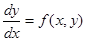, удовлетворяющего условию 
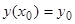. Аналогичный вопрос возникает и для уравнений вида 
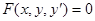. Очевидно, что для таких уравнений через некоторую точку 
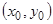, вообще говоря, проходит уже не одна, а несколько интегральных кривых, так как, разрешая уравнение 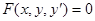относительно 
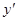мы, как правило, получаем не одно, а несколько действительных значений 
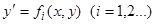, и если каждое из уравнений 
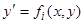в окрестности точки 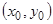удовлетворяет условиям теоремы существования и единственности, доказанной ранее, то для каждого из этих уравнений найдется единственное решение, удовлетворяющее условию 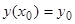. Поэтому свойство единственности решения уравнения 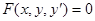, удовлетворяющего условию 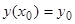, обычно понимается в том смысле, что через данную точку 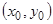по данному направлению проходит не более одной интегральной кривой уравнения .
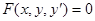Например, для решений уравнения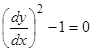 
свойство единственности всюду выполнено, так как через каждую точку 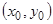проходят две интегральные кривые, но по различным направлениям. Действительно, 
, 
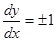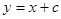и 
.
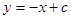Для уравнения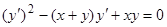 
, которое мы уже рассматривали в начале прошлой темы, в точках прямой 
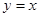свойство единственности нарушено, так как через точки этой прямой проходят интегральные кривые уравнени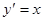й 
и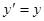 
по одному и тому же направлению.
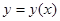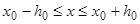Теорема. Существует единственное решение 
, 
, где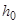 
достаточно мало, уравнения
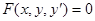, (1)
удовлетворяющее условию 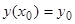, для которого 
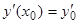, где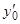 
— один из действительных корней уравнения 
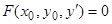, если в замкнутой окрестности точки 
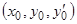функция 
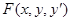удовлетворяет условиям:
1) 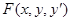непрерывна по всем аргументам;
2) производная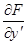 
существует и отлична от нуля;
3) существует ограниченная по модулю производная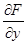 
, 
.
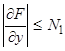Доказательство. Согласно известной теореме о существовании неявной функции можно утверждать, что условия 1) и 2) гарантируют существование единственной непрерывной в окрестности точки 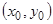функции 
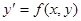, определяемой уравнением (1) и удовлетворяющей условию 
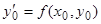. Остается проверить, будет ли функция 
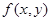удовлетворять условию Липшица 
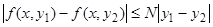, где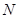 
— постоянная, или же более грубому условию 
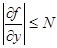в окрестности точки 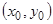, так как тогда можно будет утверждать, что уравнение
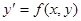(2)
удовлетворяет условиям ранее доказанной теоремы существования и единственности и, следовательно, существует единственное решение уравнения (2), удовлетворяющее условию 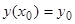, а вместе с тем существует единственная интегральная кривая уравнения (1), проходящая через точку 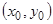и имеющая в ней угловой коэффициент касательной .
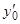Согласно известной теореме о неявных функциях можно утверждать, что при выполнении условий 1), 2), 3) производная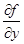 
существует и может быть вычислена по правилу дифференцирования неявных функций.
Дифференцируя тождеств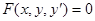о по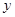 
и принимая во внимание, что 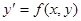, получим 
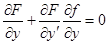, или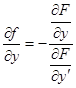 
, откуда, принимая во внимание условия 2) и 3), следует, что 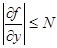в замкнутой окрестности точки .
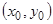Множество точек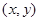 
, в которых нарушается единственность решений уравнения (1), называется особым множеством.
В точках особого множества должно быть нарушено по крайней мере одно из условий теоремы, которую мы только что доказали. В дифференциальных уравнениях, встречающихся в прикладных задачах, условия 1) и 3) обычно выполняются, но условие 2)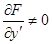 
часто нарушается.
Если условия 1) и 3) выполнены, то в точках особого множества должны одновременно удовлетворяться уравнения
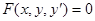и 
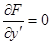. (3)
Исключая из этих уравнений 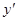, получим уравнение
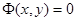, (4)
которому должны удовлетворять точки особого множества. Однако не в каждой точке, удовлетворяющей уравнению (4), обязательно нарушается единственность решения уравнения (1), так как условия теоремы лишь достаточны для единственности решения, но не являются необходимыми и, следовательно, нарушение какого-нибудь условия теоремы не обязательно влечет за собой нарушение единственности.
Итак, только среди точек кривой 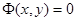, называемой р-дискриминантной кривой (так как уравнения (3) чаще записываются в виде 
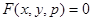и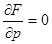 
), могут быть точки особого множества.
Если какая-нибудь ветвь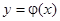 
кривой 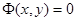принадлежит особому множеству и в то же время является интегральной кривой, то она называется особой интегральной кривой, а функция 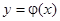называется особым решением.
Итак, для нахождения особого решения уравнения (1) надо найти р -дискриминантную кривую, определяемую уравнениями 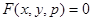, , 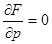выяснить путем непосредственной подстановки в уравнение (1), есть ли среди ветвей р-дискриминантной кривой интегральные кривые, и если такие кривые есть, то еще проверить, нарушена ли в точках этих кривых единственность или нет. Если единственность нарушена, то такая ветвь р-дискриминантной кривой является особой интегральной кривой.
Пример 1. Имеет ли уравнение Лагранжа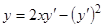 
особое решение?
Условия 1) и 3) теоремы существования и единственности выполнены. р-дискриминантная кривая определяется уравнениями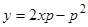 
, 
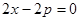, или, исключая 
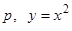. Парабола 
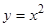не является интегральной кривой, так как функция 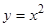не удовлетворяет исходному уравнению. Особого решения нет.
Пример 2. Найти особое решение уравнения Лагранжа
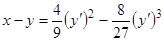. (5)
Условия 1) и 3) теоремы существования и единственности выполнены. р-дискриминантная кривая определяется уравнениями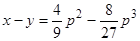 
, 
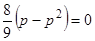. Из второго уравнения находим 
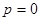или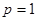 
; подставляя в первое уравнение, получим 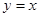или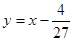 
. Лишь вторая из этих функций является решением исходного уравнения.
Для того, чтобы выяснить, будет ли решение 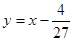особым, надо проинтегрировать уравнение (5) и выяснить, проходят ли через точки прямой 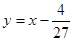по направлению этой прямой интегральные кривые. Интегрируя уравнение Лагранжа (5), получим
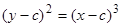. (6)
Из уравнения (6) и видно, что прямая 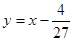является огибающей семейства полукубических парабол 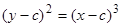и, следовательно, в каждой точке прямой 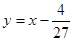нарушена единственность — по одному и тому же направлению проходят две интегральные кривые: прямая 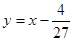и касающаяся этой прямой в рассматриваемой точке полукубическая парабола.
Итак, особым решением является 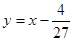. В этом примере огибающая семейства интегральных кривых является особым решением.
Если огибающей семейства
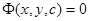(7)
называть кривую, которая в каждой своей точке касается некоторой кривой семейства (7) и каждого отрезка которой касается бесконечное множество кривых рассматриваемого семейства, то огибающая семейства интегральных кривых некоторого уравнения 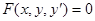всегда будет особой интегральной кривой.
Действительно, в точках огибающей значения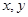 
и 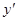совпадают со значениям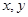и и 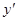для интегральной кривой, касающейся огибающей в точке 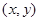, и следовательно, в каждой точке огибающей значения 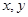и 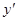удовлетворяют уравнению 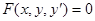, т.е. огибающая является интегральной кривой. В каждой точке огибающей нарушена единственность, так как через точки огибающей по одному направлению проходят по крайней мере две интегральные кривые: огибающая и касающаяся ее в рассматриваемой точке интегральная кривая семейства (7). Следовательно, огибающая является особой интегральной кривой.
Зная семейство интегральных кривых 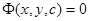некоторого дифференциального уравнения 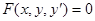, можно определить его особые решения путем нахождения огибающей. Как известно из курса дифференциальной геометрии либо матанализа, огибающая входит в состав с-дискриминантной кривой, определяемой уравнениям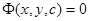и и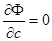 
, однако, кроме огибающей, в состав с-дискриминантной кривой могут входить и другие множества, например, множество кратных точек кривых рассматриваемого семейства, в которых 
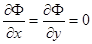. Чтобы некоторая ветвь с-дискриминантной кривой заведомо была огибающей, достаточно, чтобы на ней:
1) существовали ограниченные по модулю частные производные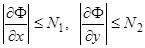 
;
2) 
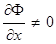или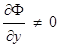 
.
Заметим, что эти условия лишь достаточны, так что кривые, на которых нарушено одно из условий 1), 2), тоже могут быть огибающими.
Пример 3. Дано семейство интегральных кривых 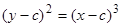некоторого дифференциального уравнения (см. пример 2 этой темы). Найти особое решение того же уравнения.
Находим с-дискриминантную кривую: 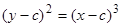и 
. И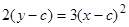сключая параметр 
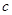, получим 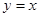и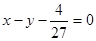 
. Прямая 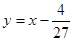является огибающей, так как на ней выполнены все условия теоремы об огибающей. Функция 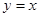не удовлетворяет дифференциальному уравнению. Прямая 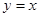является геометрическим местом точек возврата. В точках этой прямой нарушено второе условие теоремы об огибающей.
Пример 4. Дано семейство интегральных кривых
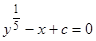(8)
некоторого дифференциального уравнения первого порядка. Найти особое решение того же уравнения.
Задача сводится к нахождению огибающей рассматриваемого семейства. Если непосредственно применить указанный выше метод нахождения огибающей, то получим противоречивое уравнение 1=0, откуда казалось бы естественно сделать вывод, что семейство (8) не имеет огибающей. Однако в данном случае производная левой части уравнения (8) по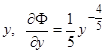 
, обращается в бесконечность при 
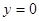, и следовательно, не исключена возможность того, что 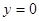будет огибающей семейства (8), которую не удалось найти общим методом ввиду нарушения на прямой 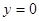условий теоремы.
Следует преобразовать уравнение (8) так, чтобы для преобразованного уравнения, эквивалентного исходному, уже выполнялись условия теоремы об огибающей. Например, запишем уравнение (8) в виде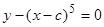 
. Теперь условия теоремы об огибающей выполнены, и, применяя общий метод, получим 
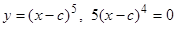, или, исключая 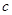, будем иметь уравнение огибающей .
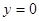Пример 5. Дано семейство интегральных кривых
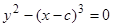(9)
некоторого дифференциального уравнения первого порядка. Найти особое решение того же уравнения.
с-дискриминантная кривая определяется уравнениям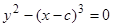и и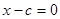 
, или, исключая 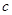, получим 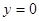. На этой прямой обращаются в нуль обе частные производные 
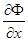и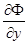 
левой части уравнения (9), следовательно, 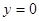является геометрическим местом кратных точек кривых семейства (9), в данном случае точек возврата. Однако это геометрическое место точек возврата в рассматриваемом примере является одновременно и огибающей.
