Лекция 5
Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид
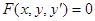 . (1)
. (1)
Если это уравнение удается разрешить относительно 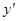 , то получаем одно или несколько уравнений
, то получаем одно или несколько уравнений 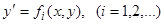 . Интегрируя эти, уже разрешенные относительно производной уравнения, найдем решения исходного уравнения (1).
. Интегрируя эти, уже разрешенные относительно производной уравнения, найдем решения исходного уравнения (1).
Проинтегрируем, например, уравнение
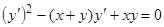 . (2)
. (2)
Разрешая это квадратное уравнение относительно 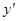 , будем иметь:
, будем иметь: 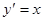 и
и 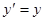 . Интегрируя каждое из полученных уравнений, находим:
. Интегрируя каждое из полученных уравнений, находим:
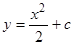 (3)
(3)
и
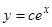 (4)
(4)
. Оба семейства решений удовлетворяют исходному уравнению.
Гладкими интегральными кривыми уравнения (2) будут также кривые, составленные из дуги интегральной кривой семейства (3) и дуги интегральной кривой семейства (4), если в общей точке они имеют общую касательную.
Еще пример. 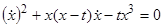 .
.
Представим данное уравнение в виде 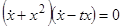 . Отсюда исходное уравнение эквивалентно совокупности двух уравнений:
. Отсюда исходное уравнение эквивалентно совокупности двух уравнений: 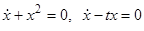 . Решение первого из них
. Решение первого из них 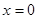 и
и 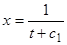 , а второго —
, а второго — 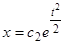 .
.
Итак, уравнение (1) может быть проинтегрировано путем разрешения относительно 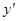 и интеграции полученных при этом уравнений
и интеграции полученных при этом уравнений 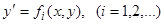 , уже разрешенных относительно производной.
, уже разрешенных относительно производной.
Однако далеко не всегда уравнение (1) легко разрешается относительно 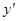 и еще реже полученные после разрешения относительно
и еще реже полученные после разрешения относительно 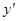 уравнения
уравнения 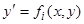 легко интегрируются, поэтому часто приходится интегрировать уравнения вида (1) иными методами. Рассмотрим следующие случаи.
легко интегрируются, поэтому часто приходится интегрировать уравнения вида (1) иными методами. Рассмотрим следующие случаи.
1. Уравнение (1) имеет вид
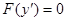 , (5)
, (5)
причем существует по крайней мере один действительный корень 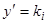 этого уравнения.
этого уравнения.
Так как уравнение (5) не содержит  и
и 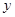 , то
, то 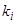 — постоянное. Следовательно, интегрируя уравнение
— постоянное. Следовательно, интегрируя уравнение 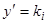 , получим
, получим 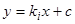 , или
, или 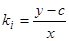 , но
, но 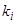 является корнем уравнения (5), следовательно,
является корнем уравнения (5), следовательно, 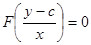 является интегралом рассматриваемого уравнения.
является интегралом рассматриваемого уравнения.
Пример 1. 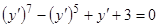 .
.
Интеграл этого уравнения — 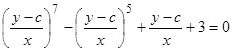 .
.
2. Не всегда уравнение (1) разрешается относительно производной и еще реже полученные после разрешения относительно производой уравнения легко интегрируются. Поэтому уравнения вида (1) часто приходится решать методом введения параметра.
а) Пусть уравнение 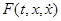 можно разрешить относительно
можно разрешить относительно  , т.е. записать в виде
, т.е. записать в виде 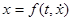 . Введя параметр
. Введя параметр 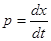 , получим
, получим 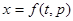 . Взяв полный дифференциал от обеих частей последнего равенства и заменив на основании введения параметра
. Взяв полный дифференциал от обеих частей последнего равенства и заменив на основании введения параметра 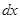 на
на 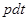 , получим уравнение
, получим уравнение
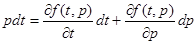 ,
,
т.е. уравнение вида 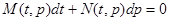 . Если найдем решения этого уравнения в виде
. Если найдем решения этого уравнения в виде 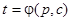 , то, воспользовавшись
, то, воспользовавшись 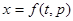 , получим решения исходного уравнения в параметрической форме:
, получим решения исходного уравнения в параметрической форме: 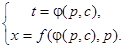
б) Пусть уравнение 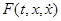 можно разрешить относительно
можно разрешить относительно 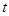 , т.е. записать в виде
, т.е. записать в виде 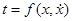 . Введя параметр
. Введя параметр 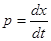 , получим
, получим 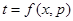 . Взяв полный дифференциал от обеих частей последнего равенства и заменив, в силу введения параметра,
. Взяв полный дифференциал от обеих частей последнего равенства и заменив, в силу введения параметра, 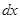 на
на 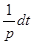 , получим уравнение
, получим уравнение
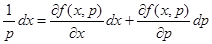 ,
,
т.е. уравнение вида 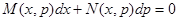 . Если найдем решения этого уравнения в виде
. Если найдем решения этого уравнения в виде 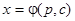 , то воспользовавшись
, то воспользовавшись 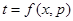 , получим решения исходного уравнения в параметрической форме:
, получим решения исходного уравнения в параметрической форме: 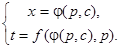
Пример. 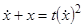 .
.
Это уравнение разрешаем относительно 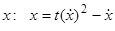 . Введем параметр
. Введем параметр 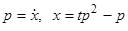 . Из равенств
. Из равенств 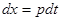 и
и 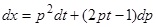 получим
получим 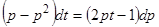 . Последнее уравнение имеет очевидные решения
. Последнее уравнение имеет очевидные решения 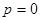 и
и 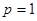 . Остальные его решения найдем, записав уравнение в виде
. Остальные его решения найдем, записав уравнение в виде
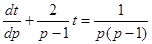 .
.
Это уравнение является линейным. Решая его, находим 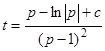 . Таким образом, решения исходного уравнения имеют вид
. Таким образом, решения исходного уравнения имеют вид 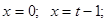

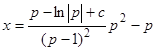 .
.
3. Уравнение (1) имеет вид
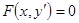 . (6)
. (6)
Если это уравнение трудно разрешить относительно 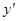 , то целесообразно ввести параметр
, то целесообразно ввести параметр 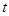 и заменить уравнение (6) двумя уравнениями:
и заменить уравнение (6) двумя уравнениями: 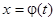 и
и 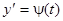 . Так как
. Так как 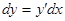 , то в данном случае
, то в данном случае 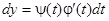 , откуда
, откуда 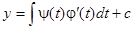 и, следовательно, интегральные кривые уравнения (6) определяются в параметрической форме следующими уравнениями:
и, следовательно, интегральные кривые уравнения (6) определяются в параметрической форме следующими уравнениями:
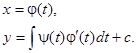
Если уравнение (6) легко разрешимо относительно 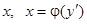 , то почти всегда удобно в качестве параметра ввести
, то почти всегда удобно в качестве параметра ввести 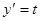 . Тогда
. Тогда
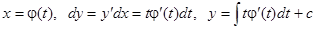 .
.
Пример 2. 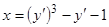 .
.
Положим 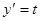 , тогда
, тогда
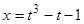 , (7)
, (7)
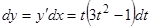 ,
,
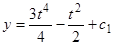 . (8)
. (8)
Уравнения (7) и (8) определяют в параметрической форме семейство искомых интегральных кривых.
Пример 3. 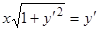 .
.
Полагаем 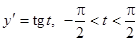 ; тогда
; тогда
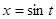 , (9)
, (9)
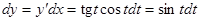 ,
,
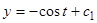 (10)
(10)
или, исключая 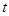 из уравнений (9) и (10), получим
из уравнений (9) и (10), получим 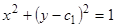 — семейство окружностей.
— семейство окружностей.
4. Уравнение (1) имеет вид
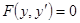 . (11)
. (11)
Если это уравнение трудно разрешить относительно 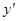 , то, как и в предыдущем случае, целесообразно ввести параметр
, то, как и в предыдущем случае, целесообразно ввести параметр 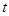 и заменить уравнение (11) двумя уравнениями:
и заменить уравнение (11) двумя уравнениями: 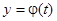 и
и 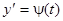 . Так как
. Так как 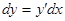 , то
, то 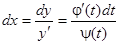 , откуда
, откуда 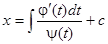 . Следовательно, искомые интегральные кривые в параметрической форме определяются уравнениями
. Следовательно, искомые интегральные кривые в параметрической форме определяются уравнениями 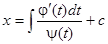 и
и 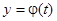 .
.
В частности, если уравнение (11) легко разрешимо относительно 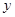 , то обычно за параметр удобно взять
, то обычно за параметр удобно взять 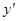 .
.
Действительно, если 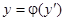 , то, полагая
, то, полагая 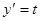 , получим
, получим 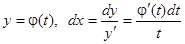 .
.
Пример 4. 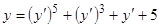 .
.
Полагаем 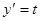 ; тогда
; тогда
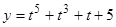 , (12)
, (12)
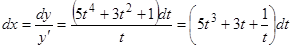 ,
,
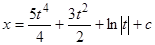 . (13)
. (13)
Уравнения (12) и (13) являются параметрическими уравнениями семейства интегральных кривых.
Пример 5. 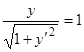 .
.
Полагаем 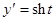 , тогда
, тогда
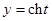 , (14)
, (14)
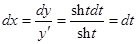 ,
,
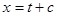 (15)
(15)
или, исключая из (14) и (15) параметр 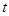 , получаем
, получаем 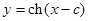 .
.
Рассмотрим теперь общий случай: левая часть уравнения (1) зависит от всех трех аргументов 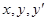 . Заменим уравнение (1) его параметрическим представлением:
. Заменим уравнение (1) его параметрическим представлением:
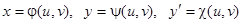 .
.
Пользуясь зависимостью 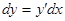 , будем иметь
, будем иметь
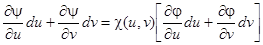 ,
,
откуда, разрешая относительно производной 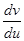 , получим
, получим
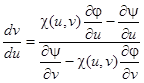 . (16)
. (16)
В результате получено уравнение первого порядка, уже разрешенное относительно производной, и тем самым задача сведена к уже рассмотренной ранее. Однако, конечно, уравнение (16) далеко не всегда будет интегрироваться в квадратурах.
Если уравнение (1) легко разрешимо относительно  , то за параметры
, то за параметры 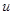 и
и 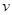 часто удобно брать
часто удобно брать  и
и 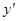 . Действительно, если уравнение (1) приводится к виду
. Действительно, если уравнение (1) приводится к виду
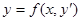 , (17)
, (17)
то, считая  и
и 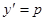 параметрами, получим
параметрами, получим 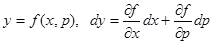 , или
, или
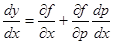 ,
,
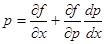 . (18)
. (18)
Интегрируя уравнение (18) (опять же, конечно, оно далеко не всегда интегрируется в квадратурах), получим 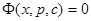 . Совокупность уравнений
. Совокупность уравнений 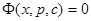 и
и 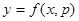 , где
, где 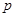 — параметр, определяет семейство интегральных кривых.
— параметр, определяет семейство интегральных кривых.
Заметим, что уравнение (18) может быть получено дифференцированием уравнения (17) по  . Действительно, дифференцируя (17) по
. Действительно, дифференцируя (17) по  и полагая
и полагая 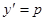 , получим
, получим 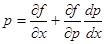 , что совпадает с (18). Поэтому этот метод часто называют интегрированием дифференциальных уравнений с помощью дифференцирования.
, что совпадает с (18). Поэтому этот метод часто называют интегрированием дифференциальных уравнений с помощью дифференцирования.
Совершенно аналогично часто интегрируется уравнение (1), если оно легко разрешимо относительно  :
:
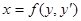 . (19)
. (19)
В этом случае, взяв за параметры 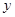 и
и 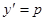 и пользуясь зависимостью
и пользуясь зависимостью 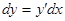 , получим
, получим 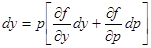 или
или
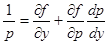 . (20)
. (20)
Интегрируя уравнение (20), получим 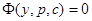 . Это уравнение совместно с
. Это уравнение совместно с 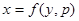 определяет интегральные кривые исходного уравнения. Уравнение (20) может быть получено из уравнения (19) дифференцированием по
определяет интегральные кривые исходного уравнения. Уравнение (20) может быть получено из уравнения (19) дифференцированием по 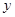 .
.
В качестве примера применения этого метода рассмотрим линейное относительно  и
и 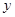 уравнение
уравнение
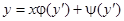 ,
,
называемое уравнением Лагранжа. Дифференцируя по  и полагая
и полагая 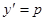 , получим
, получим
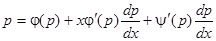 , (21)
, (21)
или
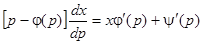 . (22)
. (22)
Это уравнение линейно относительно  и
и 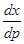 и, следовательно, легко интегрируется, например, методом вариации произвольной постоянной. Получив интеграл
и, следовательно, легко интегрируется, например, методом вариации произвольной постоянной. Получив интеграл 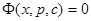 уравнения (22) и присоединяя к нему
уравнения (22) и присоединяя к нему 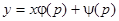 , получим уравнения, определяющие искомые интегральные кривые.
, получим уравнения, определяющие искомые интегральные кривые.
При переходе от уравнения (21) к уравнению (22) пришлось делить на 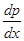 . Но при этом мы потеряем решения, если они существуют, для которых
. Но при этом мы потеряем решения, если они существуют, для которых 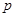 постоянно, а значит
постоянно, а значит 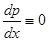 . Считая
. Считая 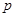 постоянным, замечаем, что уравнение (21) удовлетворяется лишь в том случае, если
постоянным, замечаем, что уравнение (21) удовлетворяется лишь в том случае, если 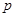 является корнем уравнения
является корнем уравнения 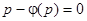 .
.
Итак, если уравнение 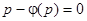 имеет действительные корни
имеет действительные корни 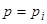 , то к найденным выше решениям уравнения Лагранжа надо еще добавить
, то к найденным выше решениям уравнения Лагранжа надо еще добавить 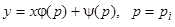 , или, исключая
, или, исключая 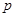 ,
, 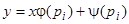 — прямые линии.
— прямые линии.
Отдельно надо рассмотреть случай, когда 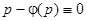 , и следовательно, при делении на
, и следовательно, при делении на 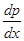 теряется решение
теряется решение 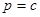 , где
, где 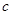 — произвольная постоянная. В этом случае
— произвольная постоянная. В этом случае 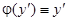 и уравнение
и уравнение 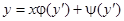 принимает вид
принимает вид 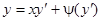 — уравнение Клеро. Полагая
— уравнение Клеро. Полагая 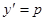 , получим
, получим 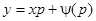 . Дифференцируя по
. Дифференцируя по  , будем иметь:
, будем иметь: 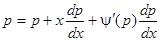 , или
, или 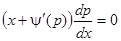 , откуда или
, откуда или 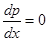 , и, значит,
, и, значит, 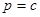 , или
, или 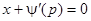 .
.
В первом случае, исключая 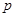 , получим
, получим
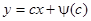 (23)
(23)
— однопараметрическое семейство интегральных прямых. Во втором случае решение определяется уравнениями
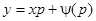 и
и 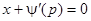 . (24)
. (24)
Нетрудно проверить, что интегральная кривая, определяемая уравнениями (24), является огибающей семейства интегральных прямых (23).
Действительно, огибающая некоторого семейства 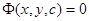 определяется уравнениями
определяется уравнениями
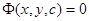 и
и 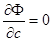 , (25)
, (25)
которые для семейства 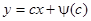 имеют вид
имеют вид 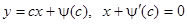 и лишь обозначением параметра отличаются от уравнений (24).
и лишь обозначением параметра отличаются от уравнений (24).
Как известно, уравнения (25) могут определять, кроме огибающей, геометрические места кратных точек, а иногда и другие кривые, однако если хотя бы одна из производных 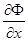 и
и 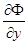 отлична от нуля и обе ограничены в точках, удовлетворяющих уравнениям (25), то эти уравнения определяют только огибающую. В данном случае эти условия выполнены:
отлична от нуля и обе ограничены в точках, удовлетворяющих уравнениям (25), то эти уравнения определяют только огибающую. В данном случае эти условия выполнены: 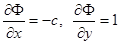 . Следовательно, уравнения (25) определяют огибающую, которая может выродиться в точку, если семейство (23) является пучком прямых.
. Следовательно, уравнения (25) определяют огибающую, которая может выродиться в точку, если семейство (23) является пучком прямых.
Пример 6. 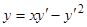 — уравнение Клеро.
— уравнение Клеро.
Однопараметрическое семейство интегральных прямых имеет вид 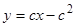 . Кроме того, интегрально кривой является огибающая этого семейства, определяемая уравнениями
. Кроме того, интегрально кривой является огибающая этого семейства, определяемая уравнениями 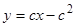 и
и 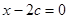 . Исключая
. Исключая 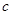 , получаем
, получаем 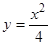 .
.
Пример 7. 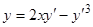 — уравнение Лагранжа.
— уравнение Лагранжа.
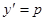 ,
,
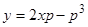 . (26)
. (26)
Дифференцируя, получаем
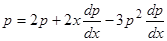 (27)
(27)
и после деления на 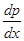 приходим к уравнению
приходим к уравнению 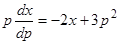 . Интегрируя это линейное уравнение, получаем
. Интегрируя это линейное уравнение, получаем 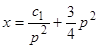 . Следовательно, интегральные кривые определяются уравнениями
. Следовательно, интегральные кривые определяются уравнениями 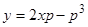 ,
, 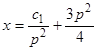 .
.
При делении на 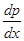 , как мы уже рассматривали, теряются решения
, как мы уже рассматривали, теряются решения 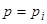 , где
, где 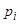 — корни уравнения
— корни уравнения 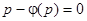 . В данном случае теряется решение
. В данном случае теряется решение 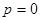 уравнения (27), которому, в силу уравнения (26), соответствует решение исходного уравнения
уравнения (27), которому, в силу уравнения (26), соответствует решение исходного уравнения 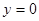 .
.
 2014-02-17
2014-02-17 6082
6082
