2014-02-17
2310
Запишем уравнения электромеханической (2.20) и механической (2.21) характеристик
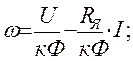
(2.20)
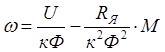. (2.21)
Все члены уравнения (2.20) разделим на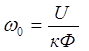 
и получим
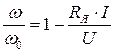. (2.22)
Второй член правой части уравнения (2.22) умножим и разделим на IНОМ
.
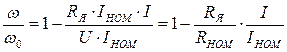Таким образом, получили
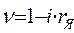, (2.23)
где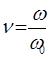 
– угловая скорость в относительных единицах;
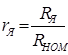– сопротивление обмотки якоря в относительных единицах;
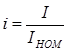– ток в относительных единицах.
Полученное уравнение (2.23) представляет собой зависимость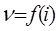 
и называется уравнением электромеханической характеристики в относительных единицах.
Проделаем то же самое с уравнением (2.21)
,
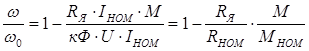и получим
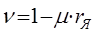, (2.24)
где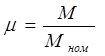 
– момент в относительных единицах.
Полученное уравнение (2.24) представляет собой зависимость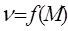
и называется уравнением механической характеристики в относительных единицах.
Построим электромеханические и механические характеристики с помощью полученных уравнений (2.23) и (2.24). Для этого достаточно знать координаты двух точек. Первая точка соответствует режиму холостого хода и имеет координаты (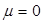
(i=0); 
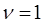). Вторая точка соответствует номинальному режиму с координатами (
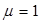(i=1); 
).
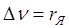Для определения координаты второй точки, а именно перепада скоростей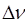 
равного сопротивлению обмотки якоря в относительных единицах
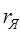, учтем, что
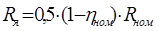, а 
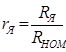
и получим
.
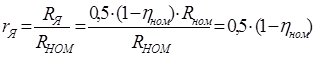Для построения реостатных характеристик в относительных единицах достаточно определить перепад скоростей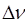в относительных единицах
.
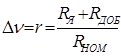На рисунке 2.8 представлены естественная и реостатная характеристики ДПТ НВ в относительных единицах.
 |
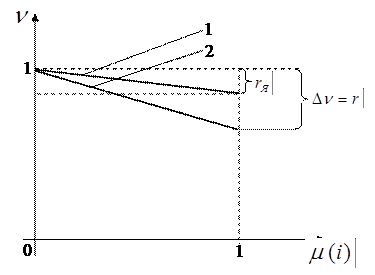Рисунок 2.8 – Естественная (1) и реостатная (2) характеристики ДПТ НВ в относительных единицах
