2014-02-17
2074
Реакция линейной системы на произвольное заданное входное воздействие также может быть определена, если известны частотные характеристики, определяющие реакцию системы на входные гармонические колебания вида:
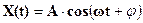, (1-27)
где А – амплитуда колебания;
w – частота колебания;
j – фазовый сдвиг.
Гармонические колебания, являясь периодической функцией времени, существуют на бесконечно большом интервале времени. Поэтому при подаче на вход физических систем периодических воздействий реакцией системы считаются только установившиеся колебания выходной величины, возникающие по прохождению достаточно большого отрезка времени после начала входного воздействия. Таким образом, если при пользовании методом переходных характеристик исследуется поведение системы в переходных процессах, то при пользовании методом частотных характеристик интересуются лишь установившимся режимом работы системы, т.е. используется принципиально отличный подход к вопросам анализа и синтеза систем управления.
При подаче на вход линейной динамической системы гармонических колебаний вида (1-27) на выходе, по истечении достаточно большого промежутка времени, возникают установившиеся колебания выходной величины, являясь гармоническими колебаниями того же вида и частоты, что и входные, но отличающиеся (в общем случае) амплитудой и фазой.
Пользуясь формулой Эйлера, можно записать гармонические функции вида (1-27) для входа и выхода в комплексной форме, удобной при анализе систем автоматического управления:
;
.
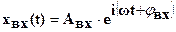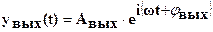Взяв отношение выходной и входной величины, получим комплексную величину, зависящую от частоты входных колебаний:
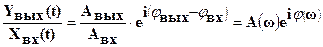(1-28)
Модуль этой комплексной величины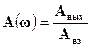 
, характеризуемый отношением амплитуд выходных и входных колебаний, с изменением частоты от 0 до ¥ меняет свою величину и называется амплитудно-частотной характеристикой (АЧХ) системы.
Аргумент комплексной величины j(w)=jвых-jвх, определяемый разностью фаз выходных и входных колебаний в зависимости от частоты, называется фазо-частотной характеристикой (ФЧХ) системы.
Комплексная функция частоты:
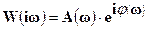(1-29)
называется комплесно-частотной характеристикой (КЧХ) системы, причем модуль ее есть амплитудно-частотная характеристика, а аргумент – фазо-частотная характеристика системы.
Зная (КЧХ) системы, легко находится (1-28) и ее реакция на гармонические колебания:
.
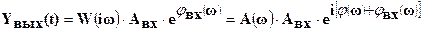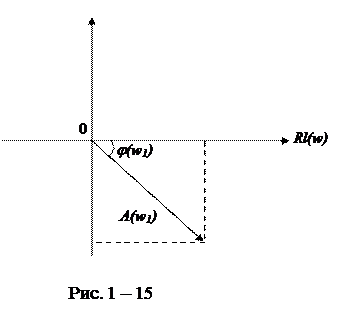На комплексной плоскости величина A×eij при какой-либо частоте изображается вектором (рис. 1 – 15), длина которого равна отношению амплитуд, а угол – разности фаз выхода и входа. Соответственно, комплексно-частотная характеристика изображается на комплексной плоскости кривой, которую очерчивает конец вектора A×eij при изменении частоты от 0 до ¥.
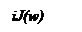Часто комплексно-фазовую характеристику записывают не только в показательном виде, но и в виде суммы вещественной и мнимой составляющих:
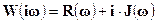, (1-30)
Связанных с амплитудно-частотной и фазо-частотной характеристиками следующими формулами:
|
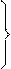
(1-31)
При известных вещественной и мнимой составляющих амплитудно-частотная и фазо-частотная характеристики легко находятся (рис. 1 – 15) по формулам:
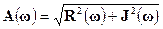; (1-32)
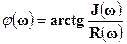. (1-33)
Необходимо отметить, что понятие комплексно-частотной характеристики системы можно получить и другим путем, исходя из дифференциального уравнения, описывающего динамические свойства линейных систем управления. Предположим, что на вход линейной динамической системы, описываемой дифференциальным уравнением
,
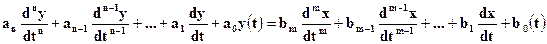подаются гармонические колебания вида: x(t)=A×ei(wt+j).
Тогда, т.к. производная входного и выходного сигнала соответственно связана с входным и выходным сигналом выражениями:
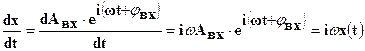; (1-34)
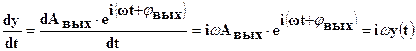(1-35)
исходное дифференциальное уравнение можно переписать в виде
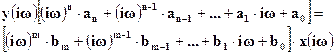(1-36)
Отсюда находим, что комплексно-частотная характеристика линейной динамической системы находится по выражению:
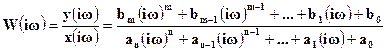(1-37)
Если сравнить полученное выражение для комплексно-частотной характеристики линейной динамической системы с выражением (1-16) для передаточной функции той же системы, то можно заключить, что формально (КЧХ) получается из передаточной функции линейной динамической системы заменой оператора Р не комплексную величину iw.
Аналогично, зная комплексно-частотную характеристику системы, легко находится реакция ее на произвольное входное воздействие, если воспользоваться преобразованиями Фурье.
В этом случае вход и выход линейной системы описываются суммой соответствующим образом подобранных гармонических функций (а не суммой элементарных ступенчатых воздействий). Причем изображение по Фурье выхода системы легко находится при известных комплексно-частотной характеристике и изображении по Фурье входного воздействия:
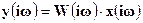. (1-38)
