Переходные характеристики

При исследовании систем автоматического управления обычно используются два вида переходных характеристик:

- переходная характеристика, называемая также кривой разгона или временной характеристикой;

- импульсная переходная характеристика, называемая также импульсной характеристикой или функцией веса.

Реакция линейной системы на единичное ступенчатое входное воздействие называется переходной характеристикой – h(t). Эта характеристика может быть получена как аналитически, так и экспериментально путем подачи на вход системы единичного ступенчатого воздействия – x₀(t) и регистрации вызванного этим воздействием значения выхода системы – h(t) (рис. 1 – 12).

Реакция линейной системы на входное воздействие в виде дельта-функции - d(t) называется импульсной переходной характеристикой W(t). Эта характеристика (пунктир на рис. 1 – 13б) может быть также получена аналитически и экспериментально.

Однако необходимо помнить, что входное воздействие в виде дельты-функции реализовать в реальных условиях не представляется возможным, так как это воздействие представляет собой бесконечно большой импульс на бесконечно малом отрезке времени, что невозможно получить из-за ограничений накладываемых реальной регулирующей аппаратурой на скорость и величину перемещения регулирующего органа. Поэтому при экспериментальном получении импульсной переходной характеристики необходимо подавать входной сигнал возможно большей величины в течение отрезка времени Dt, положительность которого определяется технологическими особенностями данной системы. Регистрация изменения выхода системы, обусловленного подачей на вход последней импульсного сигнала длительностью Dt, позволяет получить экспериментальную импульсную переходную характеристику - W^эк(t) (рис. 1 – 13), степень приближения которой к идеальной импульсной характеристике – W(t) (пунктир, рис. 1 – 13) будет определяться величиной входного сигнала и временем его действия на вход системы Dt.

Аналитически переходная и импульсная переходная характеристики системы находятся достаточно просто при знании дифференциального уравнения системы. Например, полагая, что дифференциальное уравнение системы имеет вид:

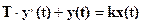, (1-19)

переходная характеристика системы находится как решение этого уравнения при единичном входном воздействии X(t)=I(t) и при начальных условиях Y(t=0)=0. Решение исходного уравнения осуществлялось в § 1-5 и, следовательно, переходная характеристика для рассматриваемой системы имеет вид (рис. 1 – 11):

.

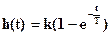Импульсная переходная характеристика рассматриваемой системы есть решение исходного дифференциального уравнения при

.

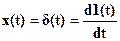Тогда, так как правая часть есть производная, существующая только в момент времени, равной 0, то при t>0 исходного уравнения – (1-19) соответствует уравнению:

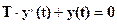, (1-20)

решение которого ищется в виде:

.

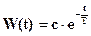Начальные условия Y(0) находятся путем интегрирования обеих частей уравнения (1-19) в пределах от –t₁ до +t₁

.

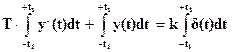Устремив - t₁®0 и +t₁®+0 получаем:

,

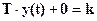отсюда находим начальное условие:

.

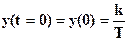В результате, решения уравнение (1-20) при найденных начальных условиях, записываем импульсную переходную характеристику линейной системы в виде:

.

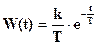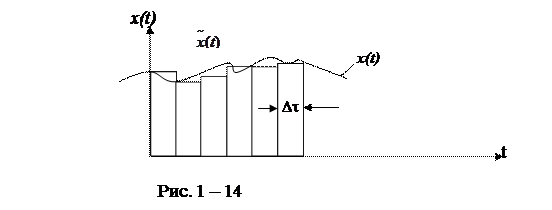
Выше отмечалось, что знание реакции линейной системы на типовое воздействие позволяет определить и реакцию линейной системы на любое другое входное воздействие, которое может быть представлено в виде суммы последовательных воздействий. Полагая, что известной является импульсная переходная характеристика линейной системы W(t), найдем значение выхода системы в момент времени t на произвольное (но заданное) входное воздействие X(t). Для этого необходимо заменить X(t) приближенным ступенчатым воздействием , с шагом каждой ступеньки по времени - Dt (рис. 1 – 14), полагая, что:

1. Функция - последовательность прямоугольных импульсов длительностью .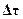

2. .

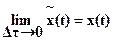Таким образом, для приближенного нахождения реакции линейной системы в момент времени t на входное воздействие x(t) необходимо знать сумму реакций системы на все прямоугольные импульсы длительностью Dt, предшествующие моменту времени. При этом степень приближения полученного результата к его истинному значению будет тем больше, чем меньше длительность импульсов - Dt.

Реакцию системы на достаточно короткий прямоугольный импульс можно считать приближенно равной импульсной переходной характеристике системы W(t), умноженной на площадь этого импульса x(t)×Dt. Следовательно, реакция системы на ступенчатое воздействие будет определяться выражением:

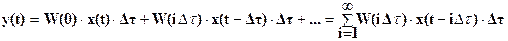. (1-21)

Устремив в формуле (1-21) Dt к 0 (т.е. Dt ® 0), можно найти точное решение поставленной задачи. При этом знак суммы заменяется интегралом, а дискретное значение времени iDt заменяется непрерывно изменяющимся значением - t:

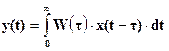(1-22)

В результате получается так называемая формула свертки, широко используемая в теории автоматического управления, а операция, осуществляемая этой формулой, называется сверткой функций W(t) и x(t).

Для физически реализуемых систем импульсные переходные характеристики должны удовлетворять условию:

W(t)=0 при t<0.

Поэтому интеграл (1-22) не изменится, если нижний предел перенести в - ¥:

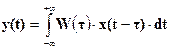. (1-23)

Как правило, при решении задач анализа и синтеза систем

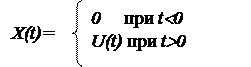автоматического управления ищется реакция динамических систем на внезапно приложенное воздействие:

Поэтому в верхнем пределе интеграла (1-22) и (1-23) можно вместо +¥ поставить t, получив тем самым наиболее распространенную форму записи интеграла свертки, т.е.

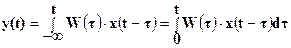(1-24)

Из последних формул легко можно определить переходную характеристику системы, полагая, что – X(t)=I(t):

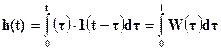. (1-25)

Таким образом, как следует из (1-25), переходная характеристика (кривая разгона) представляет собой интеграл от импульсной переходной характеристики.

С другой стороны, импульсная переходная характеристика равна первой производной от переходной характеристики:

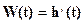(1-26)