Исследование переходных процессов методом динамических характеристик

В инженерной практике исследования систем автоматического управления не всегда целесообразно использовать метод дифференциальных уравнений из-за сложности и громоздкости последнего при решении дифференциальных уравнений высокого порядка, которыми описываются промышленные системы управления. В этих условиях предпочтительнее пользоваться методом динамических характеристик, описывающих (как и дифференциальные уравнения) свойства систем управления.

К достоинствам метода динамических характеристик, обуславливающих их широкое распространение, следует отнести следующее:

1) динамические характеристики могут быть найдены не только аналитически, но и экспериментальным путем;

2) операции с динамическими характеристиками, осуществляемые, как правило, графическим путемсущественно проще, чем операции с дифференциальными уравнениями.

Динамические характеристики определяют поведение линейной (или линеаризованной) системы при некоторых заранее заданных типовых входных воздействиях. Обычно в качестве типовых входных воздействий выбираются такие воздействия, суммой которых можно представить любое входное воздействие, могущее возникнуть в процессе работы реальной системы. В результате, согласно принципу суперпозиции, реакция линейной системы на любое входное воздействие может быть найдена суммированием с соответствующими весами реакций на выбранное типовое воздействие. Из вышеизложенного видно, что понятие «динамическая характеристика» не имеет смысла для нелинейных систем, так как последние не подчиняются принципу суперпозиции.

Как правило, в качестве входного типового воздействия используется одна из следующих функций.

1. Единичная ступенчатая функция – I(t), характеризуемая мгновенным перемещением регулирующего органа на 100% от диапазона регулирования.

2. Дельта-функция – 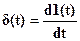– это производная от единичной ступенчатой функции, представляющая собой предел, к которому стремится импульсная функция.

3. Гармонические колебания - a×coswt+b×sinwt.

В зависимости от вида подаваемого на вход системы типового воздействия динамические характеристики линейных систем бывают:

1. Переходные характеристики, определяемые в результате подачи на вход системы типового воздействия в виде единичной ступенчатой функции или дельта-функции.

2. Частотные характеристики, определяемые в результате подачи на вход системы типового воздействия в виде гармонических колебаний.