Ортогональная классификация поверхностей второго порядка.
Ортогональная классификация кривых второго порядка
Теорема 9.3. Любая кривая второго порядка ортогонально эквивалентна одному из 9 классов кривых, приведенных в таблице. Приведенные кривые ортогонально не эквивалентны между собой.
| Название кривой | Каноническое уравнение кривой |
| Эллипс | 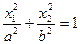
|
| Мнимый эллипс | 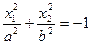
|
| Гипербола | 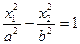
|
| Пара пересекающихся мнимых прямых | 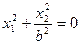
|
| Пара пересекающихся прямых | 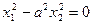 , , 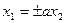
|
| Парабола | 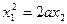
|
| Пара параллельных прямых | 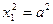
|
| Пара параллельных мнимых прямых | 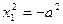
|
| Пара совпавших параллельных прямых | 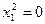
|
Доказательство. очевидно
Теорема 9.4 Любая поверхность второго порядка ортогонально эквивалентна одной из поверхностей в одном из 17 классов, приведенных в таблице. Приведенные поверхности ортогонально не эквивалентны между собой.
| Название поверхности | Каноническое уравнение поверхности |
| Эллипсоид | 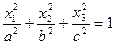
|
| Мнимый эллипсоид | 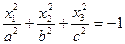
|
| Однополостный гиперболоид | 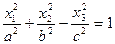
|
| Двуполостный гиперболоид | 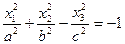
|
| Мнимый конус | 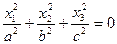
|
| Конус | 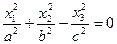
|
| Эллиптический параболоид | 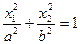
|
| Эллиптический цилиндр | 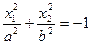
|
| Мнимый эллиптический цилиндр | 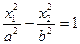
|
| гиперболический цилиндр | 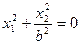
|
| Пара пересекающихся мнимых плоскостей | 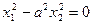 , , 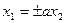
|
| Пара пересекающихся плоскостей | 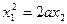
|
| Параболический цилиндр | 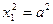
|
| Пара параллельных плоскостей | 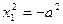
|
| Пара параллельных мнимых плоскостей | 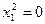
|
| Пара совпавших плоскостей | 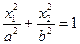
|
| Гиперболический параболоид (седло) | 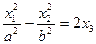
|
Доказательство очевидно.
 2014-02-17
2014-02-17 717
717







