Значение энтропии для заданного состояния определяется интегрированием уравнения
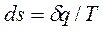
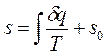 (3.5)
(3.5)
где sо — константа интегрирования.
При температурах, близких к абсолютному нулю, все известные вещества находятся в конденсированном состоянии. В. Нернст (1906 г.) экспериментально установил, а М. Планк (1912 г.) окончательно сформулировал следующий принцип: при температуре, стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю, т. е. s0=0 при T=0 К. Этот закон называют третьим законом термодинамики или тепловой теоремой Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются произвольного уровня.
Однако в технической термодинамике обычно используется не абсолютное значение энтропии, а ее изменение в каком-либо процессе:
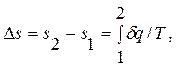 (3.6)
(3.6)
поэтому энтропию тоже часто отсчитывают от произвольно выбранного уровня.
Получим формулы, позволяющие вычислить изменение энтропии идеального газа. Для этого проинтегрируем уравнение:
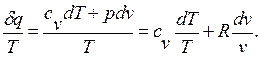 (3.7)
(3.7)
положив для простоты cv=const:
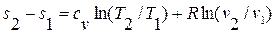 (3.8)
(3.8)
Из уравнения Клапейрона, записанного для состояний 1 и 2, следует:
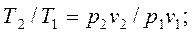
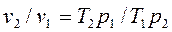 (3.9)
(3.9)
После подстановки отношений T2/T1 и v2/v1 в выражение (3.8) получим следующие формулы для изменения энтропии идеального газа:
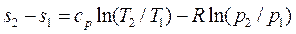 (3.10)
(3.10)
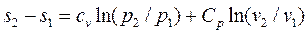 (3.11)
(3.11)
Поскольку энтропия есть функция состояния рабочего тела, уравнениями (3.8) — (3.11) можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями 1 и 2 и, в частности, от того, равновесный этот переход или нет.
 2014-02-09
2014-02-09 1106
1106








