Расстояние от точки А до точки В, отсчитанное вдоль траектории, называют пройденным путем. Иными словами, пройденный путь – это длина траектории, которую описывает материальная точка за данный промежуток времени.
Перемещением называют вектор, соединяющий начальное положение материальной точки с её конечным положением 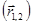 .
.
Величины, для задания которых достаточно лишь численного значения, называются скалярами. (Примеры: путь, время, масса, работа, мощность и т.д.)
Величины, характеризующиеся численным значением и направлением, называются векторами. (Примеры: перемещение, скорость, ускорение, сила, импульс и т.д.)
Положение материальной точки в пространстве можно задать при помощи радиуса-вектора 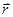 .
.
Если перемещение точки за время 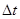 будет равно
будет равно 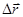 , то под скоростью точки в данный момент времени понимают предел, к которому стремится отношение
, то под скоростью точки в данный момент времени понимают предел, к которому стремится отношение 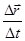 при
при 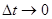 (при
(при 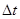 стремящемся к нулю).
стремящемся к нулю).
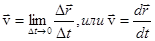 =
=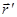 .
.
Вектор скорости направлен по касательной к траектории в соответствующей точке.
При 
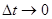 различия между элементарным путем
различия между элементарным путем 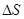 и модулем элементарного перемещения
и модулем элементарного перемещения 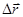 невелико, поэтому
невелико, поэтому 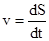 , т.е.
, т.е. 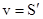 .
.
Если задана зависимость скорости от времени, то пройденный путь можно найти, пользуясь формулой
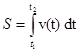

В случае прямолинейного равномерного движения 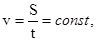
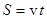 .
.
Прямолинейное равнопеременное движение. Ускорение. Физический смысл ускорения. Вычисление мгновенной скорости и пройденного пути при равнопеременном движении
Движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и ту же величину, называется равнопеременным.
Быстрота изменения скорости материальной точки характеризуется ускорением
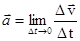 , или
, или 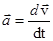 , т.е.
, т.е.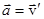 .
.
Физический смысл ускорения состоит в том, что оно является скоростью изменения скорости.
Если в начальный момент времени скорость тела равна 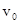 , то в любой момент времени t модуль скорости тела
, то в любой момент времени t модуль скорости тела
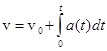 .
.
Если ускорение постоянно, то модуль мгновенной скорости 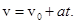
Пройденный путь (при равнопеременном движении) можно найти по формуле:
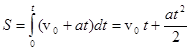 .
.
Для нахождения пройденного пути (в случае, если ускорение постоянно) также пользуются формулами:
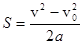 и
и 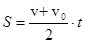 .
.
 2014-02-18
2014-02-18 5270
5270








