Применение уравнения Клапейрона – Клаузиуса к фазовым переходам

6.4.1 Качественная оценка зависимости температуры фазовых переходов от давления. Чтобы качественно оценить влияние давления на температуру фазового превращения, надо оценить знак производной 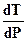. А это возможно, если известен знак теплового эффекта 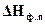и изменения объема 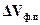(абсолютная температура имеет всегда положительный знак, т.е. 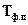> 0).

а) переход жидкость ® твердое (кристаллизация, затвердевание) идет с выделением из системы теплоты (DН < 0); для подавляющего большинства веществ (кроме воды, галлия, висмута) затвердевание сопровождается уменьшением объема (DV=V_Т -V_Ж < 0); следовательно, для них 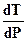> 0, т. е. уменьшение давления в системе ведет к снижению температуры кристаллизации (затвердевания) вещества и наоборот (рисунок 22, кривая 1). Например, для этилового спирта, ацетона, аммиака уменьшение давления в системе ведет к уменьшению температуры затвердевания. А увеличение давления приводит к увеличению температуры затвердевания этих веществ. А вот для воды (галлия, висмута) как аномального вещества, зависимость обратная (рисунок 22, кривая 1¹). Поэтому вода кристаллизируется (замерзает) при температуре О^оС лишь в том случае, если давление равно атмосферному (101,325 кПа). В шахте, где давление выше атмосферного, вода при О^оС не замерзает, для этого требуется более низкая температура.

б) переход жидкость ® пар (газ) сопровождается поглощениeм системой теплоты (DН > 0) и резким увеличением объема (DV > 0) [сравним объем 1 моля (18г) воды жидкой (0,018 л) и парообразной (при н. у. 22,4 л)]. Из уравнения Клапейрона – Клаузиуса следует, что 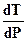> 0 (рисунок 22, кривая 2), поэтому увеличение давления ведет к увеличению температуры кипения жидкости [вода в шахте закипает не при 100^oС, как при атмосферном давлении, а при более высокой, а в горах - наоборот, при температуре менее 100^oС; аммиак при атмосферном давлении (101,325 кПа) кипит при температуре -33,4^oС, а при давлении 50 кПа закипит только при температуре -47,3^oС].

в) возгонка (т. е. переход твердого вещества в пар, минуя жидкое состояние, Т ®П) идет с поглощением теплоты (DН < 0), объем системы резко возрастает (DV > 0), следовательно, 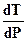> 0 (рисунок 22, кривая 3), поэтому для снижения температуры возгонки вещества необходимо уменьшить давление в системе.

Аналогичные выводы можно сделать и для обратных указанным фазовых переходов (плавления, конденсации, осаждения).

Зависимость температуры фазового перехода от давления (или давления от температуры) можно установить экспериментально и для удобства представить эту зависимость не в виде таблицы, а графически. Такой график зависимости Р=f(Т) носит название диаграммы состояния (рисунок 22).

6.4.2 Количественная оценка зависимости температуры фазовых переходов от давления. Количественную зависимость давления и температуры фазового перехода можно определить, решив уравнение (152) Клапейрона – Клаузиуса. Для приближенных расчетов можно в этом уравнении дифференциал параметров заменить на приращение:

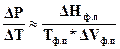. (152)

6.4.3 Определение теплоты фазовых переходов. Очень часто приходится оценивать тепловой эффект фазового превращения вещества. Наиболее удобным способом это можно сделать, используя связь давления с температурой фазового перехода. Для этого вначале экспериментально определяют зависимость температуры фазовых изменений от давления (или наоборот, влияние давления на температуру превращения) и строят участок диаграммы состояния. Затем, используя уравнение Клапейрона- Клаузиуса, определяют теплоту фазового перехода:

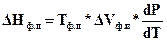, (153)

предварительно найдя величину производной 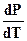графическим способом через тангенс угла наклона касательной в точке требуемых параметров P и T, как показано на рисунке 21:

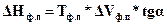. (153а)

Для приближенных расчетов можно в этом уравнении дифференциал параметров заменить на приращение:

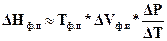. (153б)

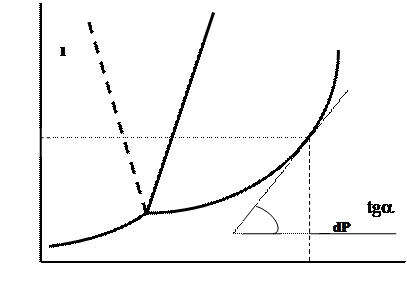Рисунок 22 - Общий вид диаграммы состояния однокомпонентной системы. Пунктирной линией (1¹) показано влияние давления на температуру плавления (кристаллизации) аномальных веществ

6.4.4 Определение истинной теплоты испарения. При испарении объем системы резко возрастает (DV=V_ПАРА-V_{ЖИДКОСТИ}@V_ПАРА), поэтому без существенной погрешности при определении изменения объема испаряющегося вещества можно объемом жидкой фазы пренебречь.

При давлении, близком к атмосферному, можно считать пар идеальным, поэтому для него:

V = (RТ)/Р.

С учетом этого соотношения уравнение (151) Клаузиуса - Клапейрона примет вид

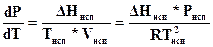. (154)

Отсюда следует, что

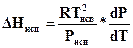, (154а)

где 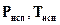- заданные значения давления (кПа) и температуры (К) фазового перехода;

R- универсальная газовая постоянная (R=8,314 Дж/(моль* К)).

Производную 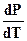определяют графическим способом (рисунок 22):

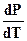= tga,

(тангенс угла определяется не по углу наклона касательной к оси температуры, а по отношению отрезков в соответствии с масштабом графика). В окончательном виде получается

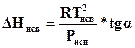. (154б)

6.4.5 Определение средней теплоты испарения жидкости. Теплоту испарения жидкости можно определить и без построения диаграммы состояния на основе упрощения уравнения (154), для чего проведем интегрирование в неопределенных пределах, принимая, что в небольшом интервале температуры DH @const [так как при выводе последующих уравнений используют некоторые допущения, то найденную теплоту испарения называют средней (усредненной), а не истинной]:

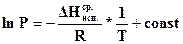, (155)

где 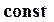- постоянная интегрирования.

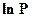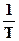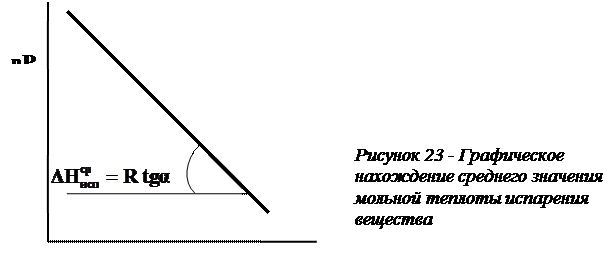
Уравнение (155) дает прямую линию в координатах - . Зная значение температур кипения хотя бы при двух давлениях, строят график 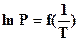и графически находят среднее значение теплоты испарения 1 моля (1 кмоля) жидкости (рисунок 23):

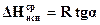. (155а)

Но можно определить 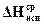и аналитически, без построения графика. Для этого проинтегрируем уравнение (154) в интервалах давления от Р₁ до Р₂, а температуры от Т₁ до Т ₂ (Т₂ > Т₁), предполагая, что DH @const (т.е. пренебрегаем небольшим приращением DН с изменением температуры):

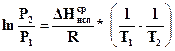, (155б)

где Т₁, Т₂ - температура кипения жидкости соответственно при Р₁ и Р₂ .

В этом случае получим уравнение, позволяющее рассчитать среднюю мольную теплоту испарения:

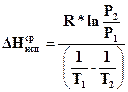. (155в)

6.5 Энтропия испарения. Мольная энтропия испарения в стандартной точке кипения (при температуре кипения 1 атм) для многих жидкостей (в частности, для неполярных веществ) примерно равна 88 Дж/(моль*К) [21 кал/ (моль*К)]:

DS_исп =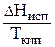»21 [кал/ (моль*К)]. (156)

Данное выражение известно как уравнение Трутона. Оно широко используется для оценки упорядоченности: если DS_исп не соответствует этому правилу, то это говорит о наличии ассоциации или диссоциации молекул жидкости.