Пусть имеется п шаров, среди которых п 1 белых и n 2 черных (п = n 1 + n 2). Выберем k элементов без возвращения. Нас интересует вероятность события А = { среди выбранных окажется k 1 белых и k 2 черных шаров (k = k 1 + k 2)}.
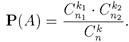 |
Общее число исходов есть число сочетаний из п элементов по k, т.е. C nk. А число исходов, благоприятствующих к событию А равно
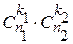 , что объясняется просто: k 1 шаров мы можем выбрать из имеющихся n 1 белых шаров
, что объясняется просто: k 1 шаров мы можем выбрать из имеющихся n 1 белых шаров 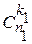 способами, a k 2черных шаров из имеющихся n 2 черных шаров
способами, a k 2черных шаров из имеющихся n 2 черных шаров 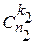 способами, при этом любой способ выбора шаров, скажем, белого цвета комбинируется с любыми способами выбора шаров черного цвета. Тогда
способами, при этом любой способ выбора шаров, скажем, белого цвета комбинируется с любыми способами выбора шаров черного цвета. Тогда
Определенные таким образом вероятности носят название гипергеометрического распределения.
Рассмотрим случай, когда среди п шаров n 1 белых, n 2 черных,..., nj красных шаров (п = n 1 + n 2 +... + nj). Выбираем k шаров так, чтобы среди них оказалось k 1 белых, k 2 черных,..., kj красных шаров (k = k 1 + k 2 +... + 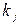 ). Событие, состоящее из таких выборок, обозначаем через А и аналогичными рассуждениями, как и в случае наличия шаров двух цветов, получаем
). Событие, состоящее из таких выборок, обозначаем через А и аналогичными рассуждениями, как и в случае наличия шаров двух цветов, получаем
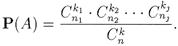 |
Пример. Из колоды в 52 карты наугад вынимаем 3 карты. Нас интересует вероятность события А = { вынуты «тройка», «семерка», «туз» }. Общее число элементарных исходов равно C 352. Исходы, благоприятные к событию А определяются так: выбирается одна «тройка» из четырех имеющихся «троек» различных мастей, одна «семерка» из четырех имеющихся «семерок» различных мастей и один «туз» из четырех имеющихся «тузов» различных мастей. Используя вышеприведенную формулу получаем
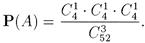 |
 2014-02-18
2014-02-18 736
736








