Независимость событий

Понятие «независимости» играет ключевую роль в теории вероятностей: оно выделило теорию вероятностей из теории меры (ибо в теории вероятностей находятся вероятности различных событий – суть измеряется мера определенного множества по сравнению с множеством единичной меры).

Однако перейдём к понятию независимости. Есл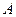и и 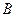два события, то естественно сказать, что событие 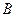не зависит от события 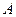, если знание того, что свершилось событие 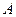, никак не влияет на вероятность события 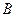. Иначе говоря (при условии >),

.

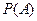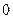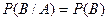По определению условной вероятности:

.

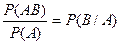Поэтому

,

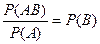откуда

.

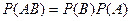Последнее равенство и принято в теории вероятностей за определение независимости двух событий.

Итак, два события 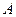и 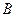называются независимыми, если

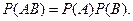
Прелесть этого определения ещё и в том, что оно годится и для случая, когда 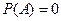(в отличие от рассуждений в начале этого пункта).

Пример. Безотказная работа прибора определяется работой двух узлов, соединённых последовательно. Вероятность безотказной работы 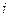-ого узла равна:

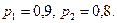
Узлы работают независимо друг от друга. Какова вероятность безотказной работы всего прибора.

Решение. Введём следующие обозначения:

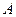- событие, состоящее в безотказной работе всего прибора;

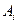- событие, состоящее в безотказной работе 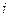-ого узла прибора ().

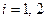Тогда в силу «последовательности» соединения

.

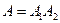Поэтому

,

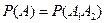а в силу независимости работы узлов прибора (вероятность произведения равна произведению вероятностей):

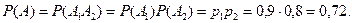
Всякое последовательное соединение приводит к потере устойчивости в работе прибора!