2#. Пусть функция 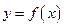 определена на интервале
определена на интервале 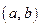 , кроме, быть может, точки
, кроме, быть может, точки 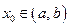 . Число
. Число 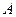 называется пределом функции
называется пределом функции 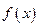 в точке
в точке 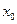 , если для любого
, если для любого 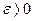 существует такое число
существует такое число 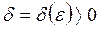 , что для всех
, что для всех 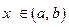 , удовлетворяющих неравенству
, удовлетворяющих неравенству 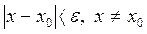 выполняется неравенство
выполняется неравенство 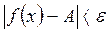 .
.
** Рассмотрим графическую интерпретацию предела функции в точке (рис.1)
! Отметим, что оба определения (по Гейне и по Коши) представляют собой определение двустороннего предела функции в точке.
Сформулируем определение односторонних преде лов – предела слева функции в точке и предела справа функции в точке.
3#. Пусть функция 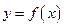 определена на полуинтервале
определена на полуинтервале 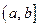 (соответственно на
(соответственно на 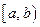 ). Число
). Число 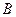 называется пределом слева (справа) функции
называется пределом слева (справа) функции 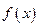 в точке
в точке 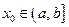 (соответственно
(соответственно 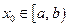 ), если для любого
), если для любого 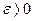 существует такое число
существует такое число 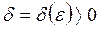 , что
, что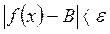 для всех
для всех 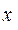 , удовлетворяющих неравенству
, удовлетворяющих неравенству  (соответственно
(соответственно 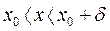 ).
).
! Обозначим: 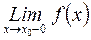 =
= 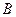 (соответственно
(соответственно 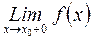 =
= 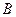 ).
).
! Отметим, что связь между односторонними пределами и двусторонним пределом устанавливает следующая теорема.
 .Функция .Функция 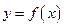 имеет предел в точке тогда и только тогда, когда в этой точке существуют пределы как справа, так и слева и они равны. В этом случае их общее значение и является двусторонним пределом функции в точке. имеет предел в точке тогда и только тогда, когда в этой точке существуют пределы как справа, так и слева и они равны. В этом случае их общее значение и является двусторонним пределом функции в точке.
|
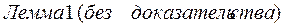 Если функция Если функция 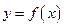 имеет предел в точке имеет предел в точке 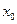 , то существует окрестность этой точки (не содержащая, быть может саму точку , то существует окрестность этой точки (не содержащая, быть может саму точку 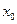 ), на которой функция ограничена. ), на которой функция ограничена.
|
 Если Если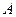 = =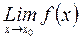 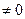 , то существует , то существует 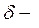 окрестность окрестность 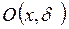 точки точки 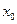 , такая, что , такая, что 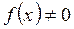 при при 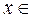 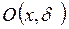 , , 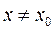 и имеет тот же знак, что и число и имеет тот же знак, что и число 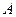 . .
|
 2014-02-18
2014-02-18 773
773








