! Отметим, что все функции, рассматриваемые в этом пункте, определены на некотором интервале 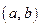 (конечном или бесконечном), кроме, быть может, фиксированной точки
(конечном или бесконечном), кроме, быть может, фиксированной точки 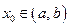 .
.
4#. Функция 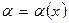 называется бесконечно малой функцие й (или просто бесконечно малой) при
называется бесконечно малой функцие й (или просто бесконечно малой) при 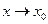 , если
, если 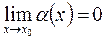 .
.
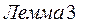 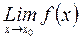 существует и равен существует и равен 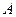 тогда и только тогда, когда тогда и только тогда, когда 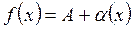 , где , где 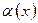 - бесконечно малая при - бесконечно малая при 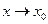 . .
|
Если 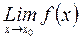 =
=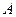 , то, полагая, что
, то, полагая, что 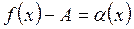 , получим
, получим 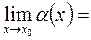
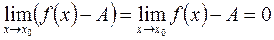 .
.
Если же верно обратное утверждение - 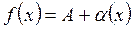 и
и 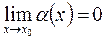 , то
, то
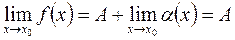 .
.
☺
Непосредственно из свойств пределов последовательностей и определения предела функции по Гейне следует теорема 2:
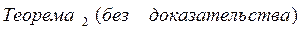 .Сумма и произведение конечного числа бесконечно малых функций при .Сумма и произведение конечного числа бесконечно малых функций при 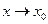 , а также произведение бесконечно малой функции при , а также произведение бесконечно малой функции при 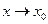 на ограниченную функцию являются бесконечно малыми функциями при на ограниченную функцию являются бесконечно малыми функциями при 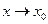 . Частное . Частное 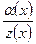 от деления функции бесконечно малой от деления функции бесконечно малой 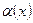 при при 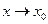 на функцию на функцию 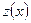 , предел которой при , предел которой при 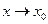 отличен от нуля, есть функция бесконечно малая. отличен от нуля, есть функция бесконечно малая.
|
5#. Функция 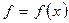 называется бесконечно большой при
называется бесконечно большой при 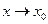 , если для любого
, если для любого 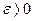 существует такое число
существует такое число 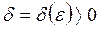 , что
, что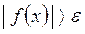 для всех
для всех 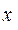 , удовлетворяющих неравенству
, удовлетворяющих неравенству 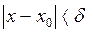 ,
, 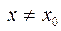 .
.
! Обозначим: 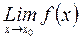 =
= 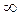 .
.
! Отметим, что если для любого 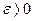 существует такое число
существует такое число 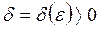 , что (соответственно
, что (соответственно 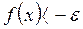 ) для всех
) для всех 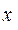 , удовлетворяющих условию
, удовлетворяющих условию 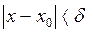 ,
, 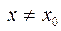 , то пишут
, то пишут
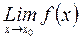 = +
= +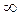 (соответственно
(соответственно 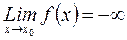 ).
).
! Отметим, что по аналогии с конечными односторонними пределами определяются и односторонние бесконечные пределы: (завершите ряд односторонних бесконечных пределов):
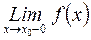 =
= 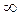 ;
; 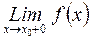 =
=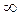 ;
; 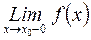 = +
= +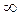 ;…
;…
До сих пор операцию предельного перехода мы рассматривали на интервале 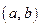 . Зададим открытый или полуоткрытый интервал, например,
. Зададим открытый или полуоткрытый интервал, например, 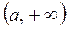 . Можно говорить о
. Можно говорить о 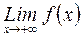 конечном пределе
конечном пределе 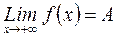 или бесконечном пределе
или бесконечном пределе 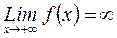 .
.
Задание. Сформулируйте определение предела 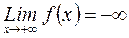 на основе предела функции по Коши.
на основе предела функции по Коши.
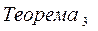 Если функция Если функция 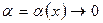 при при 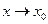 (или при (или при 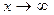 ) и не обращается в нуль, то функция ) и не обращается в нуль, то функция 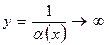 . .
|
При любом сколь угодно большом 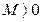 будет выполняться неравенство
будет выполняться неравенство 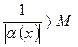 , если только будет выполняться неравенство
, если только будет выполняться неравенство 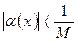 . Последнее неравенство будет выполняться для всех значений функции
. Последнее неравенство будет выполняться для всех значений функции 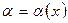 , начиная с некоторого, в силу того, что
, начиная с некоторого, в силу того, что 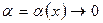 при
при 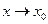 (или при
(или при 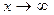 ).
).
☺
 2014-02-18
2014-02-18 667
667








