2014-02-18
599
Интегральная функция распределения
Аналитическую запись интегральной функции F (x) = P { X < x } представим в виде таблицы.
| Индекс диапазона i | Диапазон х | Значения интегральной функции F (x) |
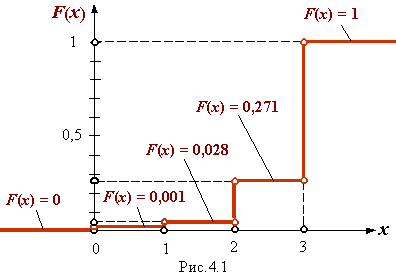
| х £ 0 | F (x (0)) = P { X <0}= 0 | |
| 0 < х £ 1 | F (x (1)) = P { X <1}= P (X =0) = 0,001 | |
| 1 < х £ 2 | F (x (2)) = P { X <2}= P (X =0) + P (X =1) = = 0,001 + 0,027 = 0,028 | |
| 2 < х £ 3 | F (x (3)) = P { X <3}= P (X =0) + P (X =1) + P (X =2) = = 0,001 + 0,027 + 0,243 = 0,271 | |
| х > 3 | F (x (4)) = P { X <4} = P (X =0) + P (X =1) + P (X =2) + P (X =3) = = 0,001 + 0,027 + 0,243 + 0,729 = 1 |
На практике при исследовании случайных величин довольно часто возникает задача определения вероятности попадания значений некоторой случайной величины Х на заданный участок [ a,b), т.е. вероятности Р { a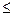 
Х < b }. Такая вероятность легко определяется с помощью интегральной функции.
Введем обозначения:
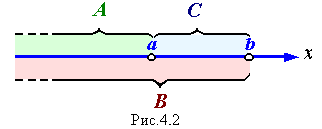
А – событие, которое заключается в том, что Х < а;
В – событие, которое заключается в том, что Х < b;
С – событие, которое заключается в том, что a 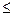Х < b.
Сложное случайное событие В представляет собой сумму событий А и С (см. рис.4.2): В = А + С.
|
|
|
Поскольку события А и С являются несовместными, то
Р (В) = Р (А) + Р (С).
