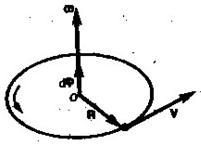
Рассмотрим движение материальной точки по окружности радиуса 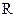 . За время
. За время 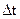 ее положение изменится на угол
ее положение изменится на угол 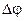 . Углы поворота рассматриваются как векторы. Модуль вектора
. Углы поворота рассматриваются как векторы. Модуль вектора 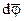 равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, то есть подчиняется правилу правого винта.
равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, то есть подчиняется правилу правого винта.
Угловой скоростью называется векторная величина, равная первой производной угла поворота по времени
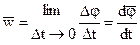 ,
,
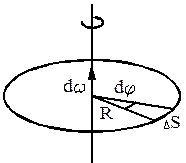
| Она направлена по оси вращения по правилу правого винта. Ее размерность [w]= с-1., а единица – рад/сек.
Линейная скорость точки равна
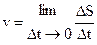 = =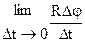 = =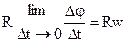
|
| Рис.5. |
| Если 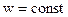 , то вращение равномерное и его можно охарактеризовать периодом обращения Т (время за которое точка совершает полный оборот, то есть поворачивается на , то вращение равномерное и его можно охарактеризовать периодом обращения Т (время за которое точка совершает полный оборот, то есть поворачивается на 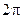 ), ), 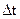 = Т соответствует = Т соответствует 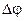 = = 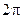 . Таким образом, . Таким образом, 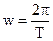 , откуда , откуда 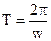 . .
|
| Рис. 6. |
Число полных оборотов за единицу времени называется частотой, 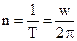 . Откуда
. Откуда 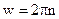 .
.
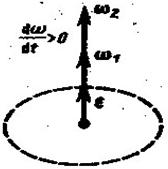
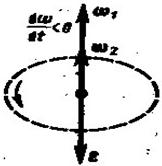
Угловым ускорением называется первая производная угловой скорости по времени, 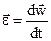 .
.
| 
|
| Рис.7. | Рис.8. |
При ускоренном движении 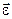 сонапрвлено с
сонапрвлено с 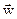 , при замедленном – противоположно направлению
, при замедленном – противоположно направлению 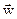 .
.
Тангенциальная составляющая ускорения равна 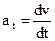 , а так как
, а так как 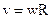 , то
, то 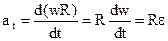 . Для нормальной составляющей имеем
. Для нормальной составляющей имеем 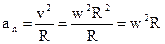 . В случае равнопеременного движения по окружности (
. В случае равнопеременного движения по окружности (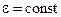 )
)
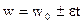 ,
, 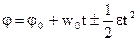 .
.
Связь между линейными и угловыми величинами:
 ,
, 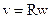 ,
, 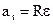 ,
, 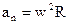 .
.
 2014-02-09
2014-02-09 665
665








