Линия тока и элементарная струйка.
Линией тока называется линия, проходящая через положения, последовательно занимаемые частицей жидкости во время ее движения.
Например, частица жидкости при движении последовательно проходит положения М1, М2, М3. Линия, соединяющая эти положения, и есть линия тока.
При установившемся движении направление движения частицы совпадает с касательной, проведенной к линии тока в данной точке.
В общем случае, при неустановившемся движении, направление движения частицы не совпадает в каждой точке с направлением линии тока.
Предположим, что давление жидкости в трубе постоянно уменьшается. В этом случае истинная траектория (показана пунктирной линией) частицы жидкости не будет соответствовать линии тока, образовавшейся в первый момент времени.
Две различные линии тока не пересекаются между собой.
Элементарной струйкой называется струя жидкости, боковая поверхность которой образована линиями тока, проходящими точки бесконечно малого замкнутого контура. Эта струя считается изолированной от окружающей ее жидкости, ее поперечное сечение бесконечно мало, длина струи не ограничена, боковая поверхность непроницаема. То есть элементарную струйку можно представить себе в виде бесконечно тонкой трубки с бесконечно малым сечением, по которому течет жидкость.
Движение может быть равномерным и неравномерным, сплошным и прерывистым.
При равномерном движении скорость потока по его длине не меняется. В противном случае движение является неравномерным.
Различают объёмный, массовый и весовой расход жидкости. Объёмный расход жидкости – это количество или объем жидкости в единицу времени.
Пусть у нас имеется элементарная струйка с поперечным сечением dω, скорость истечения жидкости в ней равна u. За время dt это сечение переместится на величину ds = u * dt.
 Следующая за ней частица жидкости заполнит освобожденное пространство и поэтому за указанный промежуток времени через поперечное сечение dω пройдет объем жидкости
Следующая за ней частица жидкости заполнит освобожденное пространство и поэтому за указанный промежуток времени через поперечное сечение dω пройдет объем жидкости
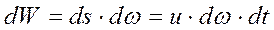
Объем жидкости, протекающий через сечение за единицу времени называют объемным расходом Q. То есть:
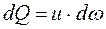
Рассмотрим движение сплошного потока жидкости. Для произвольно выбранных двух сечений потока 1-1 и 2-2 можно записать:
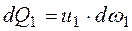
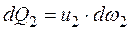
 Поскольку по условию поток сплошной, это означает, что величины расходов должны быть равны между собой, то есть количество жидкости через сечение 1 равно количеству жидкости, прошедшему через сечение 2. В противном случае в потоке должны образоваться либо пустоты, либо сгустки, что противоречит условию. То есть:
Поскольку по условию поток сплошной, это означает, что величины расходов должны быть равны между собой, то есть количество жидкости через сечение 1 равно количеству жидкости, прошедшему через сечение 2. В противном случае в потоке должны образоваться либо пустоты, либо сгустки, что противоречит условию. То есть:
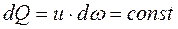
В общем случае скорость потока в различных точках поперечного сечения может быть различной, поэтому для потока вводится понятие средней по сечению скорости:
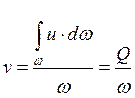 Откуда следует, что
Откуда следует, что 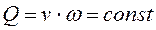
Различают напорные и безнапорные течения жидкости.
Напорными называют течения в закрытых руслах без свободной поверхности, а безнапорные – течения со свободной поверхностью. (Свободная поверхность – это граница раздела жидкости и газа, давление на которой обычно равно атмосферному.) Напорные потоки: течения в трубопроводах с повышенным (или пониженным) давлением, в гидромашинах или других гидроагрегатах. Безнапорные: течения в реках, открытых каналах, лотках.
Для характеристики потока введено понятие о живом сечении и его элементах – смоченном периметре и гидравлическом радиусе.
Живым сечением называют часть поперечного сечения канала, заполненную жидкостью.
В данном случае живое сечение потока ω меньше площади круга трубы. Если вся труба заполнена жидкостью, то живым сечением будет вся площадь круга.
Смоченным периметром называют ту часть периметра живого сечения, по которой жидкость соприкасается со стенками канала. Его обозначают буквой χ (хи).
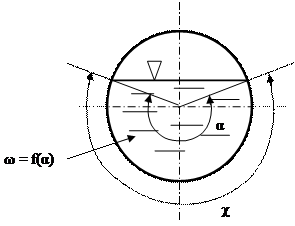 Если, например, все сечение трубы занято жидкостью, то смоченный периметр равен длине окружности внутреннего радиуса трубы.
Если, например, все сечение трубы занято жидкостью, то смоченный периметр равен длине окружности внутреннего радиуса трубы.
Гидравлическим радиусом R называют отношение живого сечения ω к смоченному периметру χ, то есть: 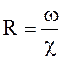
В частности, для круглых труб, заполненных жидкостью, гидравлический радиус равен четверти диаметра:
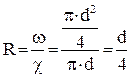
В гидромеханике и гидравлике используется понятие эквивалентный диаметр, величина которого равна четырем гидравлическим радиусам
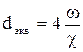 ;
;
для трубы круглого сечения 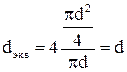 ;
;
для квадратного сечения 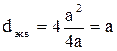 ;
;
для прямоугольного сечения 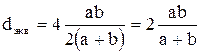 .
.
 Уравнение Бернулли.
Уравнение Бернулли.
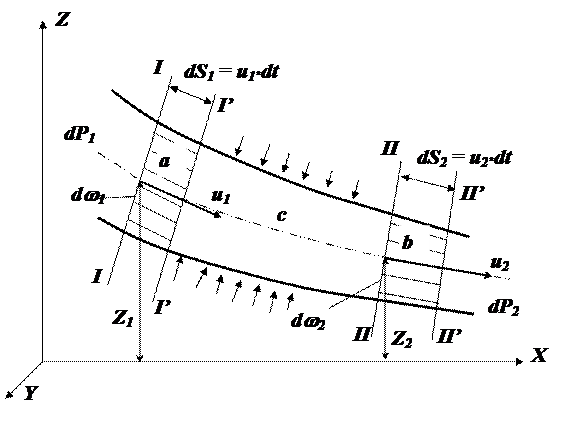
Выделим в элементарной струйке сечениями I и II некоторую одну и туже массу жидкости и составим уравнение кинетической энергии для этой массы. Учтем при этом, что приращение кинетической энергии может быть получено только за счет работы внешних сил и равно этой работе.
За время dt выделенная масса, ограниченная сечениями I-II переместится и займет сечение I’-II’. Область между этими сечениями разделим на три объема: a, b, c. При этом по условию сплошности массы объемов a и b равны между собой.
Определим приращение кинетической энергии при перемещении массы жидкости:
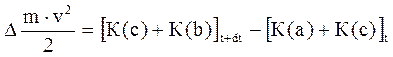
Так как движение установившееся, кинетическая энергия объема с будет постоянная. Поэтому для всей выделенной массы справедливо следующее:

Величина кинетической энергии жидкости в объеме b:
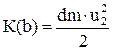
В то же время: 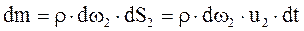
Отсюда можно записать: 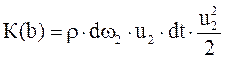
По аналогии: 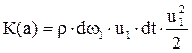
Полное приращение кинетической энергии рассматриваемой массы жидкости:
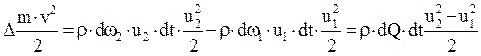
где dQ – массовый расход, независимый от сечения в соответствии с законом сохранения массы.
В случае невязкой жидкости к выделенному объему приложены силы тяжести, сила давления жидкости на боковую поверхность и силы давления на торцовые поверхности объема.
Поскольку жидкость несжимаема и мы к ней не подводим теплоту и не отводим ее, внутренняя энергия рассматриваемого объема жидкости не изменяется при его перемещении, и в уравнение кинетической энергии входит только работа внешних сил.
При перемещении выделенной массы жидкости из положения I-II в положение I’-II’ вес жидкости в объеме с работу не совершает, поскольку положение этого объема вдоль оси Z не меняется. То есть работа сил тяжести совершается только при перемещении объема а в положение жидкости, заключенной в объеме b. Эта работа выражается уравнением:
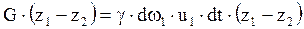
где G – вес жидкости, Z1 и Z2 – расстояния от центров тяжести соответствующих объемов.
Работа сил давления на боковую поверхность равна нулю, так как это давление перпендикулярно к рассматриваемой поверхности.
Работа сил давления на торцовые поверхности равна следующей разности
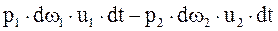
Уравнение кинетической энергии таким образом имеет следующий вид:

Разделим уравнение на dt, так как оно не равно нулю, и далее перегруппируем таким образом, что все члены, относящиеся к сечению I перенесем в левую часть, а все члены, относящиеся к сечению II – в правую:
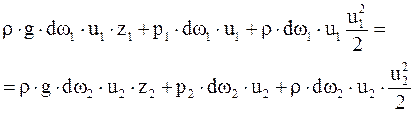
Учитывая, что: 
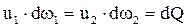
разделим уравнение на величину 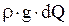
так как эта величина является константой и не равна нулю, так как входящие в него величины не равны нулю. Кроме того, учтем, что 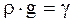
В этом случае мы получим уравнение, которое носит имя Бернулли:
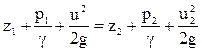 - уравнение Бернулли для элементарной
- уравнение Бернулли для элементарной
струйки идеальной несжимаемой жидкости
Если неограниченно приближать друг к другу сечения I и II, то уравнение Бернулли можно представить в дифференциальной форме:
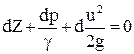 или
или 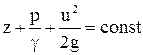
 2014-02-24
2014-02-24 1830
1830
