2014-02-24
2274
Рассмотрим поток с плавно изменяющимся течением, то есть поток, в котором элементарные струйки текут параллельно друг другу и течения в поперечном направлении отсутствует.
В этих условиях распределение давления по поперечному сечению следует закону гидростатики, то есть величина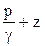 
одинакова для всех точек сечения потока.
Введём понятие мощности потока: мощность потока в данном сечении – это энергия, которую проносит поток через это сечение в единицу времени.
Рассмотрим поток как совокупность элементарных струек. Запишем выражение для мощности каждой элементарной струйки:
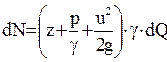
Мощность всего потока найдется интегрированием по площади поперечного сечения:
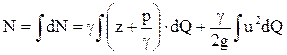
С учетом того, что поток меняется плавно, первый интеграл приводим к следующему виду:
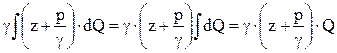
Второе слагаемое рассмотрим подробнее.
Так как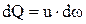 
, то можно записать:
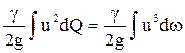
Местную скорость u можно представить в виде: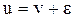 
, где v – средняя скорость, а 
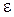- разность между средней и местной скоростью (может быть положительной, отрицательной или равной нулю). Сделав подстановку, получим:
|
|
|
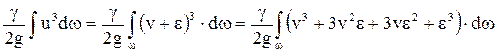
Если учесть, что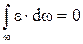 
и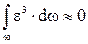 
, так как величина 
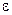очень мала и для разных точек сечения имеет различные знаки, то после перегруппировки мы получим следующее выражение:
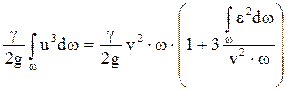
Обозначим для краткости выражение в скобках как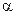 
и запишем для кинетической энергии потока выражение:
В результате для мощности всего потока имеем:
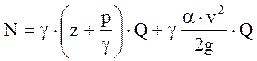
Отсюда удельная мощность потока:
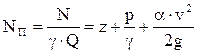
Уравнение Бернулли для потока идеальной жидкости:
,
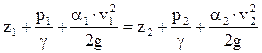или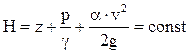 
Таким образом, уравнение Бернулли для потока отличается от такового для элементарной струйки тем, что здесь скоростной напор дополнен коэффициентом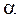 
, носящим название коэффициента Кориолиса.
Величина этого коэффициента зависит от степени неравномерности распределения скорости по сечению потока. Он всегда больше 1-цы за исключением случая, когда местные скорости равны между собой и 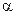=1. Для ламинарного течения в круглых трубах 
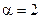, для турбулентного течения коэффициент Кориолиса принимает значение в пределах 
.
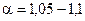Для расчета простых по сечению трубопроводов можно принимать 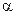=1.
