Лекция №7. Основой спектрального анализа сигналов является представление функций времени в виде ряда Фурье

Ряд, интеграл Фурье.

Основой спектрального анализа сигналов является представление функций времени в виде ряда Фурье.

В более поздние времена в начале 18 века ряд математиков (Л. Эйлер и Д.Бернулли) уже хорошо знали следующее: если каким-либо путем установить, что колебания можно выразить в виде конечной взвешенной суммы гармонически связанных между собой синусоид, то есть если будет известно, что

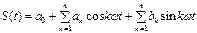
где 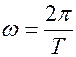, а 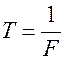, 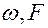основная частота, то в этом случае коэффициенты 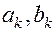можно найти из формул:

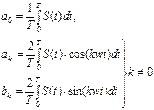
Эти результаты легко следуют из того факта, что синусоиды, чьи частоты выражаются целыми числами, кратными некоторой основной частоте 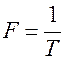, образуют множество ортогональных функций, то есть

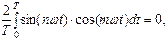при всех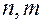

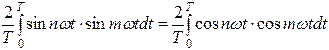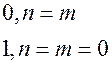
Отметим важный факт, что в форме ряда можно представить довольно ограниченный класс сигналов. В частности, поскольку

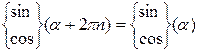то ясно, что должна быть периодической функцией с периодом повторения Т, то есть

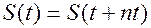
Также ясно, что любое целое число 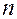периодов 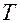также является периодом функции .

Однако даже среди периодических функций класс функций , состоящий из конечной суммы синусоид, является весьма специфичным (например, при октавном делении звукоряда одноименные звуки всех октав имеют частоты колебаний кратные частоте колебания одноименного звука нижней октавы).

Заслуга Ж.Б.Ж.Фурье состоит в том, что он в 1807 году высказал смелое предположение, что бесконечный ряд может представлять фактически любую произвольную периодическую функцию, при чем даже такую, которая содержит разрывы, то есть в форме:

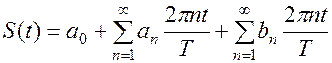
Более того, он доказал, что коэффициенты разложения такой произвольной функции могут быть найдены по тем же формулам, которые используются при представлении функций конечной суммой синусоид, то есть

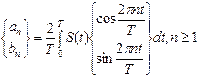
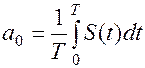
Интересно отметить, что Фурье был в большей мере инженером или физиком, а не математиком и его доказательства не удовлетворили даже современников и лишь спустя 22 года первое строгое доказательство версии теории Фурье было дано Дирихле, а строгое в современном понимании было дано почти сто лет спустя (то есть в начале двадцатого века).

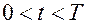В чем же состоит принципиальное отличие конечного ряда и ряда Фурье. Оказывается Фурье был полностью прав, если наложить определенные ограничения на функцию - число точек, в которых производится независимое определение в пределах периода , должно представляет собой несчетное множество, тогда как конечный ряд даже при 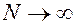содержит число независимых коэффициентов, являющихся счетным множеством.

Другие формы ряда Фурье.

Кроме тригонометрической формы записи ряда Фурье весьма полезной и пожалуй более простой является комплексная или как ее иногда называют экспоненциальная форма:

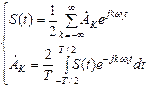
где 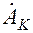- комплексная амплитуда.

Преимущество такой формы ряда Фурье, по крайней мере, в том, что для вычисления коэффициентов ряда необходимо вычислять лишь один интеграл.

Однако, следует обратить внимание на то, что сумма охватывает не только положительные значения к, но и отрицательные. Отсюда появляется понятие отрицательных частот.

Тем не менее это нисколько не усложняет ситуацию, так как, если сигнал является вещественным (а мы молчаливо это предполагаем), то из сразу же следует, что комплексная амплитуда 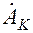- величина, комплексно сопряженная с 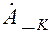, то есть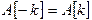

Таким образом, комплексные амплитуды компонент с отрицательной частотой определяются амплитудами компонент с положительной частотой.

Еще раз подчеркнем, что это справедливо лишь, если - вещественная функция. Если - комплексный, то естественно теряет свою справедливость.

Итак, при представлении сигнала в ряд Фурье в комплексной форме - основная задача заключается в определении комплексной амплитуды 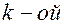гармонической составляющей.

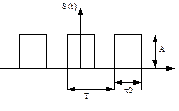
Пример: определить спектр прямоугольного колебания с периодом повторения 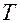, длительностью прямоугольного импульса т и амплитудой импульса .

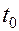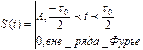
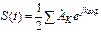, где 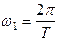-1-я гармоника

,
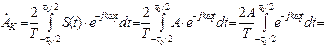
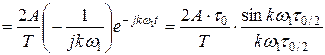
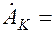
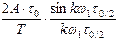
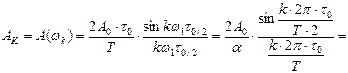
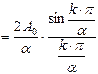при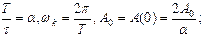

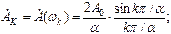
Таким образом: 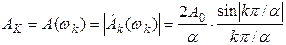, или имея ввиду, что скважность 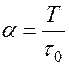, можно переписать: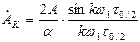

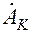- амплитудно-частотный спектр периодического сигнала.

Можно отметить следующие особенности спектра:

1) энергия постоянной составляющей обратно пропорциональна скважности;

2) энергия спектральных составляющих убывает с увеличением скважности и перераспределяется в сторону высокочастотных составляющих;

3) при целочисленных значениях 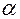все гармоники с номерами 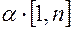равны 0. Например, при 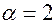, нулевые гармоники

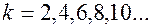при 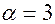, нулевые гармоники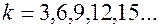

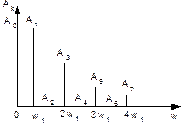
Отметим дополнительно следующее: если представляет собой действительную функцию, то следует отображать только часть спектра, соответствующую положительным частотам. Если кроме этого они является еще и четной, то есть 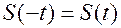, то коэффициенты 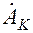являются действительными, и в этом случае ряд Фурье в тригонометрической форме содержит только косинусоиды.

Кроме этого надо знать еще и фазовый спектр 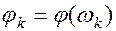,который определятся как аргумент от комплексной функции дискретного аргумента.

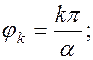при 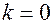, 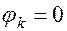и возрастает по линейному закону до .

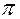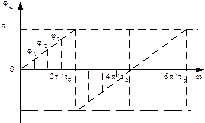
Если колебание представляет собой вещественную функцию, то есть реальный сигнал, то гармонические составляющие спектра вещественного аргумента, то есть их амплитуды, равны между собой.

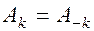
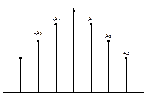
Это имеет место лишь в том случае, если сигнал вещественный. Если является комплексным, то справедливость вышеприведенного равенства не соблюдается.

Анализ показывает, что с ростом номера гармоники ее амплитуда уменьшается. При определенных значениях 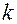амплитуду 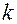-ой гармоники можно считать равной нулю, следовательно, количество гармоник, которые учитывают при рассмотрении ограничивают полосой частот 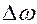, в которой содержится основная часть энергии сигнала, согласно неравенству Бесселя (или равенству Парсеваля). Эта величина называется шириной спектра.