АИМ
Импульсная несущая
Название модуляции (аналоговая и импульсная) дают по виду несущей. У импульсной несущей можно менять 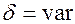 , получим широтно-импульсную модуляцию (ШИМ) Если
, получим широтно-импульсную модуляцию (ШИМ) Если 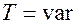 , то
, то 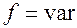 , получаем частотно-импульсную модуляцию (ЧИМ). Если
, получаем частотно-импульсную модуляцию (ЧИМ). Если 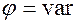 , получаем фазово-импульсную модуляцию (ФИМ).
, получаем фазово-импульсную модуляцию (ФИМ).
Т.к. по определению отдельные значения АИМ-сигналов остаются ортогональными и т.к. длительность отсчетов достаточно мала, то появляется возможность в интервале 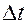 разместить
разместить 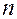 импульсных несущих.
импульсных несущих.
Т.к. 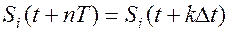 , то это – индивидуальные импульсные несущие. Импульсная несущая и ее составляющие ортогональны.
, то это – индивидуальные импульсные несущие. Импульсная несущая и ее составляющие ортогональны.
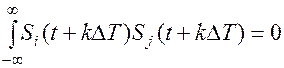 ;
; 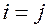 , следовательно, такая система – с временным разделением сигналов.
, следовательно, такая система – с временным разделением сигналов.
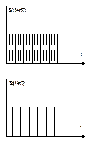
На базе таких систем можно легко построить цифровые системы.
АИМ образует несчетное (континуальное) число значений. Однако, в действительности, разрешающая способность приемных устройств конечна, поэтому передается конечное число отсчетов. К тому же, в любой линии, по определению имеется шум. Приращение сигнала, которое меньше шума передавать нет смысла, т.к. они неразличимы.
|
|
|
Таким образом, можно выбрать шаг квантования, исходя из разрешающей способности приемника, либо каких-то других соображений.
Введем понятие динамического диапазона 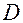 сигнала – это разница между минимальным и максимальным значениями сигнала. Значением сигнала
сигнала – это разница между минимальным и максимальным значениями сигнала. Значением сигнала 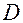 можно разбить на
можно разбить на 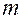 :
: 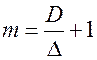 , где
, где 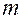 – число уровней квантования.
– число уровней квантования.
Теперь нет необходимости передавать численные значения.
Сигналы и помехи как случайные процессы

Любую функцию можно представить конечным числом точек, отстоящих на интервал Δt: 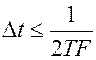
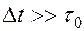 - длительность сигнала.
- длительность сигнала.
Номера уровней квантования можно передавать в десятичной системе счисления. Удобно выбрать двоичную систему счисления, которая является вероятностной.
В современных цифровых системах используется двоичное кодирование, т.е. номера сигналов можно передавать как цифровые (численные) последовательности. В групповом канале последовательности всех каналов образуют непрерывную последовательность цифр.
Спектр импульсно-модулированных сигналов определяется спектром импульсных несущих. Независимо от вида модуляции спектр импульсно-модулированных сигналов есть симметричный спектр импульсной последовательности (т.е. несущей)
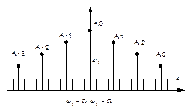
Модулированное колебание
Особенностью является спектр при АИМ, симметричный, относительно любой модулирующей составляющей, кроме нулевой. А спектр аналога модулированного сигнала определяется характером несущей составляющей.
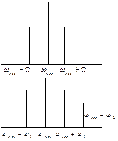
Помеха по определению – дискретный или аналоговый процесс. Разницей между сигналом и помехой нет, т.е. они описываются случайной функцией времени. Но разницы нет только в этом смысле.
|
|
|
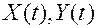 – случайные процессы.
– случайные процессы.
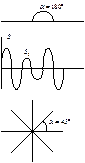 В зависимости от того, какие значения принимает случайный процесс в моменты времени
В зависимости от того, какие значения принимает случайный процесс в моменты времени  , случайные процессы подразделяют на дискретные и непрерывные.
, случайные процессы подразделяют на дискретные и непрерывные.
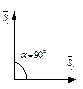
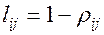
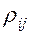 - коэффициент взаимной корреляции
- коэффициент взаимной корреляции
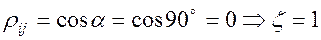 - коэффициент различимости
- коэффициент различимости
ФМ 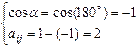
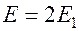
АМ 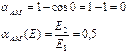
Многофазная ЧМ
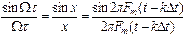 - ряд Котельникова лежит в основе систем передачи информации с временным разделением.
- ряд Котельникова лежит в основе систем передачи информации с временным разделением.
Флуктуационная помеха – множество случайных последовательностей импульсов, которые накладываются друг на друга. Флуктуационная (Гауссовская) помеха характеризуется нормальным законом распределения вероятностей амплитудных значений.
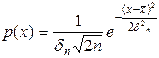
Это выражение справедливо для одномерной плотности. 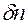 -плотность – плотность вероятности.
-плотность – плотность вероятности.
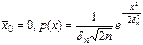
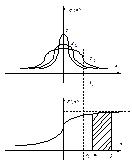
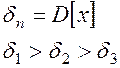
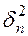 - мощность флуктуационной помехи
- мощность флуктуационной помехи
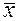 - среднее значение или постоянная составляющая;
- среднее значение или постоянная составляющая;
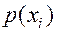 - вероятность того, что амплитудное значение флуктуационной помехи попадет в интервал
- вероятность того, что амплитудное значение флуктуационной помехи попадет в интервал 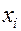 ;
;
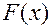 – вероятность того, что все значения флуктуационной помехи
– вероятность того, что все значения флуктуационной помехи
будут лежать левее 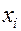 ;
;
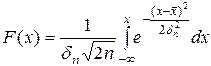 - этот интеграл вычисляется через табулированную функцию Лапласа
- этот интеграл вычисляется через табулированную функцию Лапласа 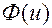 ,
,
где 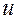 – нормированный аргумент (безразмерный)
– нормированный аргумент (безразмерный)
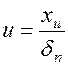 ;
;
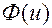 – центрированная плотность при
– центрированная плотность при 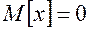 ;
;
Часто возникает задача вычисления попадания флуктуационной помехи в интервал от 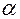 до
до 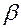 , вероятность попадания которой равна:
, вероятность попадания которой равна:
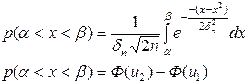
Существует несколько видов функции Лапласа: которая задается от -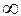 до
до 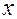 и от
и от 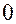 до
до 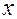 .
.
Т.к. нормальный закон распределения известен, достаточно знать параметры: среднее значение (постоянная составляющая) и среднеквадратическое отклонение (мощность помехи)
Характеристический спектр флуктуационной помехи должен быть нормально распределен.
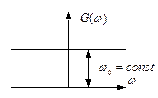
 – мощность помехи на 1 Гц частоты.
– мощность помехи на 1 Гц частоты.
Если спектр задан на бесконечном интервале, то помеха называется белым шумом, т.е. это широкополосный шум.
Если ширина шума 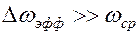 , то можно принять помеху за белый шум.
, то можно принять помеху за белый шум.
Интервал корреляции 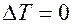 , если это идеальный белый шум, т.е. все отдельные значения этой функции независимы друг от друга, т.е. некоррелированы, и такую функцию можно назвать функцией Дирака.
, если это идеальный белый шум, т.е. все отдельные значения этой функции независимы друг от друга, т.е. некоррелированы, и такую функцию можно назвать функцией Дирака.
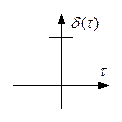
Если 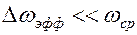 , то помеха называется окрашенным шумом.
, то помеха называется окрашенным шумом.
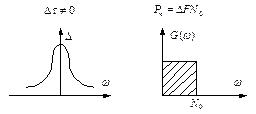
Степень случайности значений функции помехи можно определить через интервал корреляции – это интервал, на который отстают две помехи. Чем больше 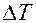 , тем процесс более случайный.
, тем процесс более случайный.
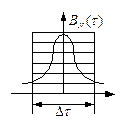
АКФ помехи.
Автокорреляционная функция – четная. Т.к. флуктуационная помеха имеет равномерный энергетический спектр, то рассматривая эту помеху в частотной области, ее можно представить в виде синфазной и противофазной частотных составляющих.
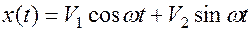 , где
, где
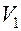 – амплитуда синфазной составляющей;
– амплитуда синфазной составляющей;
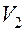 – амплитуда противофазной составляющей;
– амплитуда противофазной составляющей;
Учитывая это, можно строить приемники, в которых 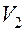 подавить. Это можно сделать с помощью когерентного приема, т.е. осуществить синхронизацию.
подавить. Это можно сделать с помощью когерентного приема, т.е. осуществить синхронизацию.
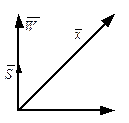
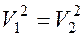
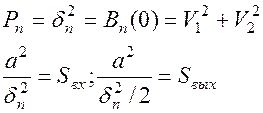
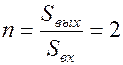 - выигрыш в отношении сигнал/шум при когерентном приеме. Выигрыш характеризует степень увеличения отношения сигнал/шум на выходе относительно отношения сигнал/шум на входе.
- выигрыш в отношении сигнал/шум при когерентном приеме. Выигрыш характеризует степень увеличения отношения сигнал/шум на выходе относительно отношения сигнал/шум на входе.
 2014-02-24
2014-02-24 2542
2542








