Биения
Биениями называется сумма двух гармонических колебаний одного направления мало различающихся по частоте.
Обозначим частоту одного из колебаний буквой w, частоту второго колебания w + Dw. По условию имеем: Dw << w. Амплитуды обоих колебаний будем полагать одинаковыми и равными а. Допустим, что начальные фазы обоих колебаний равны нулю. Тогда уравнения колебаний будут иметь следующий вид:
х 1 = а cos(w t), x 2 = a cos[(w+ Dw) t ].
Их сумма есть
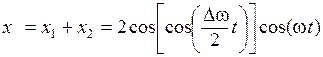 . (6.27)
. (6.27)
Во втором множители мы пренебрегли членом Dw/2 по сравнению с w. График функции (6.27) изображен на рис. 6.5, а. График построен для Dw/w= 10.
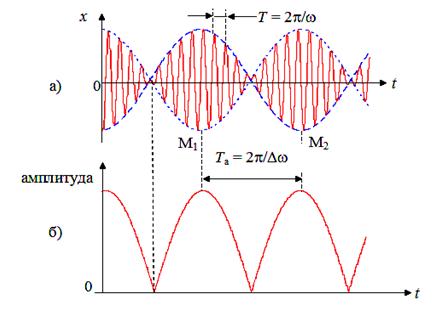
Рис. 6.5
Заключенный в квадратные скобки множитель в формуле (6.27) изменяется гораздо медленнее, чем второй множитель. Ввиду условия Dw << w за то время, за которое множитель cos(w t) совершает несколько полных колебаний, множитель стоящий в квадратных скобках, почти не изменяется. График амплитуды показан на рис. 6.5, б. Аналитическое выражение для амплитуды, очевидно, имеет вид
Амплитуда = 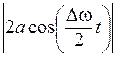 . (6.28)
. (6.28)
Функция (6.28) – периодическая функция с частотой, в два раза превышающей частоту выражения, стоящего под знаком модуля. Таким образом, частота пульсаций амплитуды – ее называют частотой биения – равна разности частот складываемых колебаний.
Допустим, что материальная точка может совершать колебания как вдоль оси X, так и вдоль перпендикулярной к ней оси Y. В этом случае, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.
Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:
х = а cos(w t), y = b cos(w t + a), (6.29)
где a – разность фаз обоих колебаний.
Выражения (6.29) представляют собой заданной в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (6.29) параметр t. Из первого уравнения следует, что
cos (w t) = x/a. (6.30)
Следовательно,
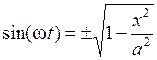 . (6.31)
. (6.31)
Теперь развернем косинус во втором из уравнений (6.29) по формуле для косинуса суммы, подставляя при этом вместо cos(w t) и sin(w t) их значения (6.30) и (6.31). В результате получим
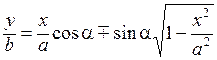 .
.
Перенося 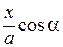 в левую часть равенства и возводя обе части в квадрат, получим
в левую часть равенства и возводя обе части в квадрат, получим
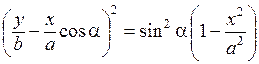 .
.
Перепишем последнее равенство в виде
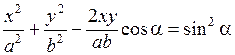 . (6.32)
. (6.32)
Уравнение (6.32) есть уравнение эллипса, оси которого повернуты относительно координатных осей х и y. Ориентация эллипса и значения его полуосей зависят довольно сложным образом от амплитуд а и b и разности фаз a.
Определим форму траектории для некоторых частных случаев.
a = 0. В этом случае уравнение (6.32) принимает вид
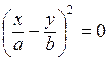 ,
,
откуда получается уравнение прямой
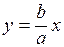 . (6.33)
. (6.33)
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой w и амплитудой, равной 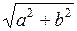 (рис. 6.6).
(рис. 6.6).
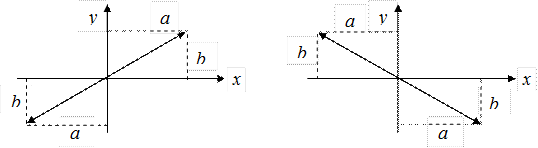
Рис. 6.6 Рис. 6.7
a = ±p. Уравнение (6.32) имеет вид
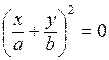 , (6.34)
, (6.34)
откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой (рис. 6.7)
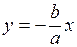 .
.
При a = ±p/2 имеем
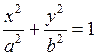 , (6.35)
, (6.35)
т. е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд a и b эллипс вырождается в окружность.
Случаи a= + p/2 и a = – p/2 различаются направлением движения по эллипсу или по окружности.
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид довольно сложных кривых называемых фигурами Лиссажу. На рис. 6.8 показана одна из простейших траекторий, получающихся при отношении частот 1:2 и разности фаз p/2. Уравнения колебаний имеют вид
x = a cos(w t), y = b cos(2w t + p/2).
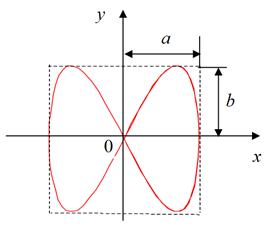
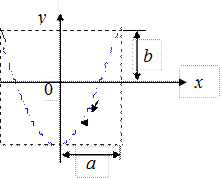
Рис. 6.8 Рис. 6.9
 2014-02-24
2014-02-24 1205
1205
