Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x, y, z и времени t:
Ψ = Ψ(x, y, z; t) (7.3)
(имеются ввиду координаты равновесного положения частицы).
Найдем вид функции Ψ в случае плоской волны, предполагая, что колебания носят гармонический характер. Для упрощения направим оси координат так, чтобы ось X совпала с направлением распространения волны. Тогда волновые поверхности будут перпендикулярными к оси x и, поскольку все точки волновой поверхности колеблются одинаково, смещение Ψ будет зависеть только от x и t: Ψ = Ψ(x, t).

Рис. 7.3
Пусть колебания точек, лежащих в плоскости x = 0 (рис.7.3), имеют вид
Ψ(0, t) = a cos(w t + a).
Найдем вид колебания точек в плоскости, соответствующей произвольному значению x. Для того чтобы пройти путь от плоскости x = 0до этой плоскости, волне требуется время t = x /u(u - скорость распространения волны). Следовательно, колебания частиц, лежащих в плоскости x, будут отставать по времени на tот колебаний частиц в плоскости x = 0, т. е. будут иметь вид
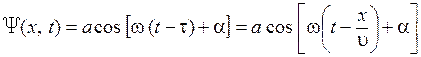 .
.
Итак, уравнение плоской волны (и продольной, и поперечной), распространяющейся в направлении оси x, выглядит следующим образом:
Ψ 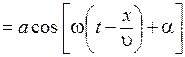 . (7.4)
. (7.4)
Зафиксируем какое либо значение фазы, стоящей в уравнении (7.4), положив
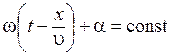 . (7.5)
. (7.5)
Это выражение определяет связь между временем t и тем местом x, в котором фаза имеет зафиксированное значение. Вытекающее из него значение dx / dt дает скорость, с которой перемещается данное значение фазы. Продифференцировав выражение (7.5), получим
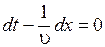 ,
,
откуда
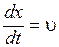 . (7.6)
. (7.6)
Таким образом, скорость распространения волны u в уравнении (7.4) есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.
Согласно (7.6) dx / dt > 0. Следовательно, уравнение (7.4) описывает волну, распространяющуюся в сторону возрастания x. Волна, распространяющаяся в противоположном направлении, описывается уравнением
Ψ 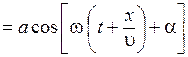 . (7.7)
. (7.7)
Уравнению плоской волны можно придать симметричный относительно x и t вид. Для этого введем величину
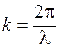 , (7.8)
, (7.8)
которая называется волновым числом. Умножив числитель и знаменатель выражения (7.8) на частоту v, можно представить волновое число в виде
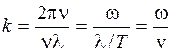 . (7.9)
. (7.9)
Раскрыв в (7.4) круглые скобки и приняв во внимание (7.9), придем к следующему уравнению плоской волны, распространяющемуся вдоль оси x:
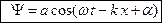 . (7.10)
. (7.10)
Уравнение волны, распространяющейся в сторону убывания x, отличается от (7.10) только знаком при члене kx:
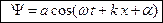 . (7.11)
. (7.11)
Теперь найдем уравнение сферической волны. Всякий реальный источник волн обладает некоторой протяженностью. Однако, если ограничится рассмотрением волны на расстояниях от источника, значительно превышающих его размеры, то источник можно считать точечным. В изотропной и однородной среде волна, порождаемая точечным источником, будет сферической. Допустим, что фаза колебаний источника равна 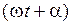 . Тогда точки, лежащие на волновой поверхности радиуса r, будут колебаться с фазой
. Тогда точки, лежащие на волновой поверхности радиуса r, будут колебаться с фазой 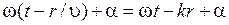 (чтобы пройти путь r, волне требуется время t = r /u). Амплитуда колебаний в этом случае убывает с расстоянием от источника по закону 1/ r.
(чтобы пройти путь r, волне требуется время t = r /u). Амплитуда колебаний в этом случае убывает с расстоянием от источника по закону 1/ r.
Следовательно, уравнение сферической волны имеет вид

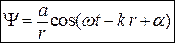 , (7.12)
, (7.12)
где a - постоянная величина, численно равная амплитуде на расстоянии от источника, равном единице.
Рассмотрим более общий случай плоской волны, распространяющийся в произвольном направлении. Для этого введем единичный вектор n нормали к волновой поверхности.
Вектор 
k = k n, (7.13)
равный по модулю волновому числу 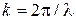 и имеющий направление нормали к волновой поверхности, называется волновым вектором. Общее уравнение плоской волны можно представить в виде
и имеющий направление нормали к волновой поверхности, называется волновым вектором. Общее уравнение плоской волны можно представить в виде
Ψ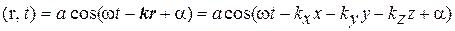 . (7.14)
. (7.14)
Мы получили уравнение плоской незатухающей волны, распространяющейся в направлении, определяемом волновым вектором k.
 2014-02-24
2014-02-24 4975
4975
