Волновое уравнение

Уравнение любой волны является решением дифференциального уравнения, называемого волновым.

Установим его вид. Для этого найдем вторые частные производные по координатам и времени от функции (7.14):

,

,

,

.

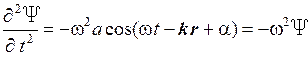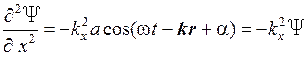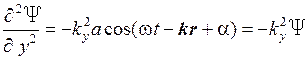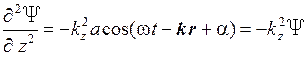Сложение производных по координатам дает

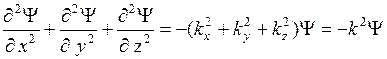. (7.15)

Сопоставив эту сумму с производной по времени и заменив 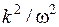через 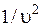(см. (7.9)), получим волновое уравнение

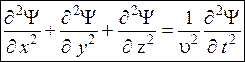. (7.16)

Легко убедится в том, что волновому уравнению удовлетворяет функция (7.14).

Для плоской волны, распространяющейся вдоль оси X, волновое уравнение имеет вид

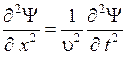. (7.17)