При решении практических задач, связанных со с.в., часто оказывается необходимым вычислять вероятность того, что с.в. примет значение, заключенное в некоторых пределах, например, от  до
до 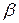 . Это событие мы будем называть попаданием с.в. на участок от
. Это событие мы будем называть попаданием с.в. на участок от  до
до 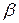 . Условимся для определенности левый конец
. Условимся для определенности левый конец  включать в участок (
включать в участок ( ,
, 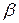 ), а правый не включать. Тогда попадание с.в. Х на участок (
), а правый не включать. Тогда попадание с.в. Х на участок ( ,
, 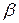 ) равносильно выполнению неравенства
) равносильно выполнению неравенства

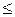 Х <
Х <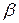 .
.
Выразим вероятность этого события через функцию распределения
величины Х. Для этого рассмотрим 3 события:
событие А, состоящее в том, что Х< 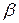 ;
;
событие B, состоящее в том, что X<  ;
;
событие C, состоящее в том, что 
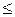 X <
X < 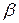 .
.
 Учитывая, что А = В + С, по теореме сложения вероятностей имеем
Учитывая, что А = В + С, по теореме сложения вероятностей имеем
Р (Х < 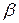 ) = P (X<
) = P (X<  ) + P (
) + P (
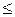
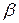 ); или
); или
F (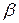 ) = F (
) = F ( ) + P (
) + P (
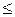 X <
X < 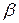 ); откуда
); откуда
P (
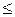 X <
X < 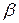 ) = F (
) = F (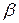 ) – F (
) – F ( ),
),
т.е. вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке.
Следствие из этого вывода: вероятность любого отдельного значения н.с.в. равна нулю, т.е. при 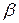
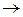
 Р(Х) = 0.
Р(Х) = 0.
 2014-02-24
2014-02-24 496
496








