2014-02-24
3134
РАЗДЕЛ 3. БЕСКОНЕЧНО МАЛЫЕ И ДР. ВЕЛИЧИНЫ
Def. Величина f (x) называется бесконечно малой при x ® a, если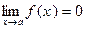 
.
(Обозначается: f (x) = o (1), читается: f (x) есть О-малое от единицыили f (x) есть бесконечно малая величина).
f (x) = o (1): Û aÎ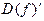
$
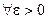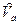
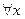Î D (f) | xÎ
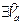Þ | f (x)| < e.
*. Cуществование конечного предела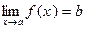 
равносильно утверждению, что функция 
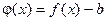есть бесконечно малая величина при x ® a.
*. Если 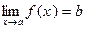то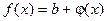 
, где j (x) = o (1) при x ® a.
Примеры:
10. 
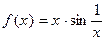. Для указанной функции f (x) = o (1) при 
.
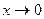20.
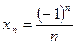. Для данной последовательности xn = o (1) при n ® +¥.
Def. Если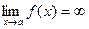 
, то величина 
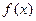называется бесконечно большой величиной.
*. Если функция имеет предел равны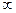й +
или -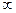, то она является бесконечно большой, но бесконечно большая величина не обязательно стремиться к бесконечности определенного знака, т.е.: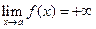 
.
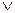
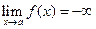
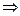
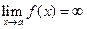Примеры:
10. 
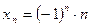Для данной последовательности 
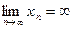бесконечно большая величина.
20. 
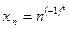. Элементы этой последовательности: 1, 2, 1/3, 4, 1/5, 6,…
Величина не ограниченна, хотя бесконечно большой не является.
Def. Числовая функция называется ограниченной сверху, снизу, ограниченной если таковым является её множество значений.
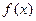ограничена сверху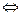 
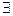M 
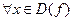
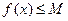
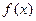ограничена снизу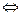 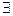m 
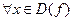
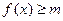
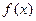ограничена m, M 
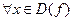
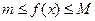
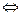
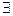A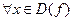 
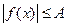
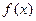неограничена сверху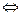 
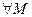
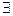
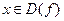
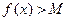
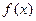неограничена снизу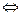 
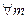
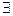
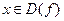
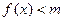
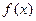неограничена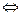 
.
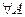
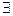
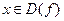
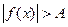
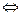
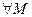
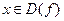
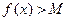
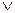
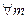
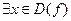
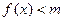Def. Числовая функция называется ограниченной …. на множестве 
, если таковым является её сужение на множество .
Сужение: f (x)| X = f (x)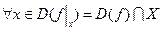 
).
Def. Функция 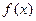называется (финально) ограниченной … в точке 
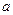сгущения её области определения если 
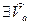на которой функция ограничена …
f (x) ограничена … - ограничена в любой точке и на любом множестве.
f (x) неограничена … в некоторой точке или на некотором множестве
- неограниченна.
В данном определении вместо многоточия указывается характер ограниченности (сверху, снизу, …).
Ограниченность функции обозначается f (x) = O (1), (читается: f (x) есть О-большое от единицыили f (x) есть ограниченная величина).
Примеры:
10. 
.
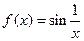ограничена сверху, снизу, ограничена сама по себе, в любой точке на любом множестве.
20. 
.
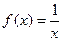На (0,1) - ограничена снизу, неограниченна сверху.
На [1,100) - ограничена сверху, ограничена снизу, ограничена.
На [-1,1] - неограничена сверху, неограничена снизу, неограничена.
Def. Величина 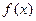называется отделенной от нуля если
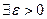
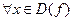
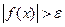
Def. Функция 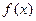называется отделенной от нуля на множестве если таково её сужение на .
Def. Функция 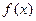финально отделена от нуля в точке 
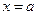если 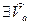такая, что функция отделена от нуля в этой проколотой окрестности.
*. Функция отделена от нуля 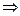отделена от нуля на любом подмножестве и в любой точке. Но…отделена от нуля в каждой точке не обязательно отделена от нуля.
*. Ненулевая бесконечно малая не отделена от нуля.
*. Функция, имеющая в точке ненулевой предел финально отделена от нуля в этой точке.
*. Если 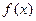отделена от нуля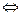 
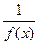- ограничена.
Примеры:
10. 
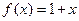2 (место для рисунка) отделена от нуля.
20. f (x) = x 2 Для " x ¹ 0 функция финально отделена от нуля.
