РАЗДЕЛ 4. НЕПРЕРЫВНЫЕ ФУНКЦИИ
§ Арифметические действия над непрерывными функциями. суперпозиция непрерывных функций
T0. Сумма, произведение и частное непрерывных функций непрерывны (частное при условии, что знаменатель отличен от нуля).
∆ 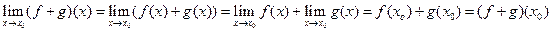 .
.
(для произведения и частного аналогично).▲
Следствия:
10.Любая натуральная степень непрерывна: 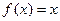 непрерывна
непрерывна 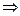
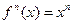 . непрерывна.
. непрерывна.
20.Любой многочлен 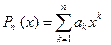 непрерывен.
непрерывен.
30.Любая рациональная функция 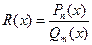 непрерывна в своей области определения.
непрерывна в своей области определения.
T0.Суперпозиция непрерывных функций непрерывна.
∆ Справедливость следует из теоремы о пределе сложной функции▲
Def. Сужением функции на множество 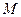 или ограничением функции
или ограничением функции 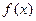 на множество
на множество 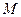 называется:
называется:
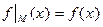
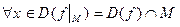 .
.
Def. Частичным пределом функции 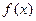 по множеству
по множеству 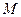 называется предел ограничения этой функции на множество
называется предел ограничения этой функции на множество 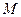 .
.
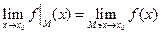 .
.
T0. Если в точке 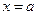 существует предел функции, то в этой точке существует и равен ему всякий частичный предел, о котором имеет смысл говорить.
существует предел функции, то в этой точке существует и равен ему всякий частичный предел, о котором имеет смысл говорить.
∆ 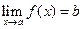
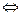
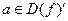
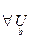
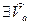
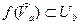
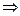
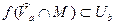 ,
,
а это значит, что: 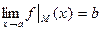 ▲
▲
Примечание: Из существования частичного предела и, даже, бесконечного числа равных частичных пределов не следует существование предела функции.
Пример: 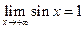 ,
, 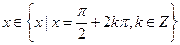 , но
, но 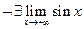 .
.
Т° (об односторонних пределах). Если существуют и равны между собой оба односторонних предела, то существует и равен их общему значению предел функции в данной точке.
∆ 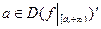
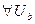
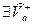
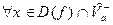
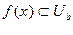 ,
,
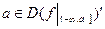
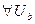
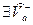
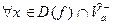
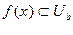 .
.
Возьмём 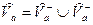 и получим
и получим 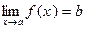 ▲
▲
 2014-02-24
2014-02-24 1208
1208








