Т°. Если существуют и конечны пределы стоящие справа в следующих равенствах, то также существуют и конечны пределы, стоящие слева и равенства выполняются:
10.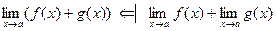 ,
,
20.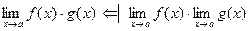 ,
,
30.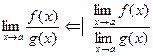 если
если 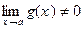 .
.
∆ 10. Пусть 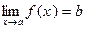 ,
, 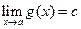 .
.
Тогда 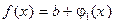 и
и 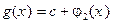 , где
, где 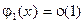
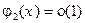 .
.
Следовательно: 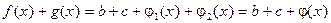 и j(x) бесконечно мала.
и j(x) бесконечно мала.
Значит 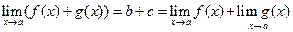 .
.
20,30 доказываются аналогично. ▲
Т°. (о пределе сложной функции).
Пусть 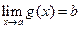 ;
; 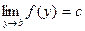 . Тогда
. Тогда 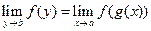 .
.
∆ По условию теоремы: 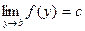 Û
Û 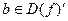 " U c
" U c 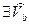
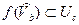 ,
,
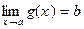 Û
Û  " Ub
" Ub 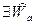
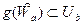 .
.
Получаем:
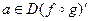
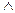 " U c
" U c 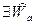
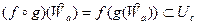
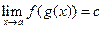
что и т. д.▲
Def. Действия с несобственными элементами:
* 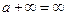 *
* 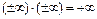 *
* 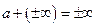
* 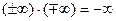 *
* 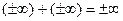 *
* 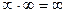
* 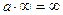 (если
(если 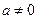 ) *
) * 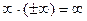
*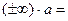
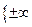 е.
е. 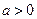 ,
, 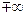 е.
е. 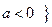
* 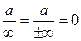 *
* 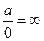 е.
е. 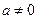 *
* 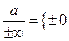 е.
е.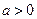 ,
, 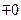 е.
е. 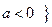 .
.
∆. Докажем например что 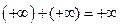
Пусть 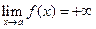 и
и 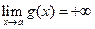
Тогда 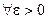
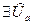
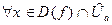
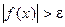 ,
,
и 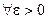
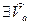
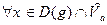
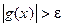 .
.
Теперь возьмём 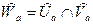 .
.
Получим:
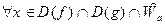
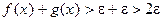 что и т. д.
что и т. д.
аналогично доказываются остальные соотношения.▲
Введя операции над несобственными элементами, обратим внимание на то, что не всяким действиям с несобственными элементами даны определения. В таких случаях говорят, что мы имеем дело с неопределенностями. Неопределенностями они называются потому, что результат этих действий может быть различным в зависимости от величин учавствующих в операции.
Рассматривается (пока) четыре типа неопределённостей:
¥-¥, 0×¥, 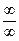 ,
, 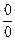 .
.
Первые две неопределённости сводятся, путем арифметических преобразований, к последним двум, а для раскрытия последних двух предназначено правило Лопиталя:
Правило: Если функции и обе стремятся к нулю или бесконечности, то предел отношения функций равен пределу отношения производных этих функций, если предел стоящий справа существует и конечен. 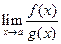 Ü|
Ü| 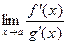 . ∆ ▲
. ∆ ▲
Конечно, такая формулировка правила Лопиталя, мягко говоря, оставляет желать лучшего. Аккуратная формулировка и доказательство этого, очень важного и удобного в применении правила будет приведено несколько позже, по мере нашей готовности к этому. Формулировка же приводится для того, чтобы позволить применять это правило, пусть и в весьма приблизительном виде, для вычисления пределов.
 2014-02-24
2014-02-24 459
459








