Бином Ньютона

Приведем и докажем очень важную формулу, предназначенную для возведения суммы двух слагаемых в натуральную степень. Эта формула называется формулой бинома Ньютона.

.

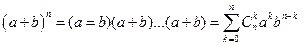∆ Доказательство теоремы проведем по методу математической индукции:

а) При 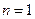имеем

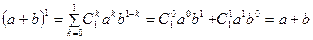
т. е. при равенство выполняется.

б) Допустим равенство выполняется при 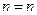т.е. .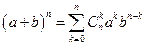

Рассмотрим: =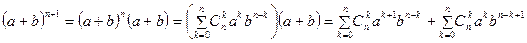

==

==

==…

…=.

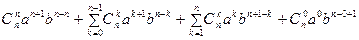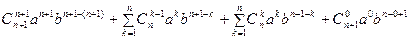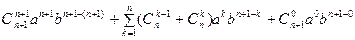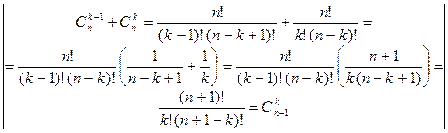
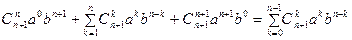
т.е. из справедливости формулы при 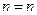следует её справедливость при 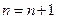. По методу математической индукции формула бинома Ньютона доказана. ▲

Следствия из формулы бинома Ньютона:

, .

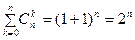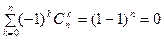1 Свойство сочетаний: ,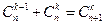

1 1 полученное выше

1 2 1 даёт способ вычисления коэффициентов

1 3 3 1 разложения 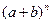. Эти коэффициенты

1 4 6 4 1 называются биноминальными.

1 5 10 10 5 1 Этот способ демонстрирует, так называемый,

… … … …... треугольник Паскаля: