Пределом функции f (x) по последовательности { xn } называется 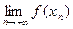 .
.
Пример: Рассмотрим 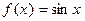 . Для этой функции
. Для этой функции 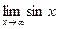 не существует.
не существует.
Однако при 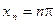
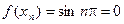 и, следовательно,
и, следовательно, 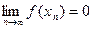 .
.
Т°. Если существует предел функции f (x) по всякой последовательности
xn ® a (xn Î D (f)) отличной от а то все эти пределы равны и существует
равный их общему значению предел функции в точке а.
∆
а) Пусть: xn ® a (xn ¹ a) и 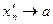 (
(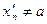 ).
).
и пусть: 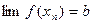 ;
; 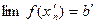 ; и
; и 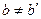 .
.
Рассмотрим новую последовательность 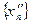 такую, что:
такую, что: 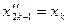 а
а 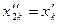 (k Î N) т.е. между элементами последовательности
(k Î N) т.е. между элементами последовательности 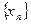 вставим элементы последовательности
вставим элементы последовательности 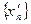 .
.
Учитывая, что 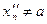 , для этой последовательности получим:
, для этой последовательности получим: 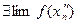 .
.
Но … 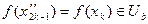 начиная с некоторого номера k 1.
начиная с некоторого номера k 1.
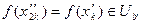 начиная с некоторого номера k 2.
начиная с некоторого номера k 2.
Тогда 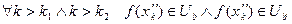 .
.
Из свойства отделимости точек числовой прямой следует, что 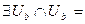 Æ и значит не существует
Æ и значит не существует 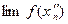 , если
, если 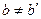 .Значит:
.Значит: 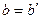 .
.
б) Пусть теперь 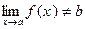 . Здесь b общее значение пределов функции по всем последовательностям. Тогда:
. Здесь b общее значение пределов функции по всем последовательностям. Тогда:
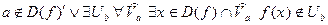 .
.
Построим последовательность 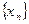 такую, что:
такую, что: 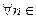 N
N 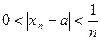 .
.
Для нее 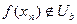 и, следовательно,
и, следовательно, 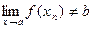 , что вновь противоречит условию теоремы. Как говорится, противоречие доказывает теорему. ▲
, что вновь противоречит условию теоремы. Как говорится, противоречие доказывает теорему. ▲
Доказанная теорема свидетельствует о том, что:
Предел функции по Гейне и по Коши – понятия эквивалентные.
§ Число e.
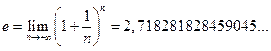
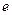 -иррациональное число.
-иррациональное число.
∆ Рассмотрим последовательность 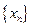 :
:
10. 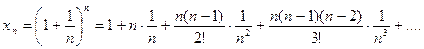
+…+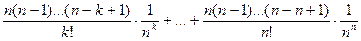 =
=
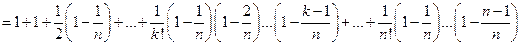 .
.
Тогда:
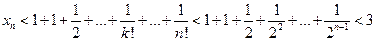 .
.
Из последнего неравенства следует, что:
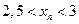 .
.
Т.е. последовательность 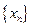 -ограничена.
-ограничена.
20. 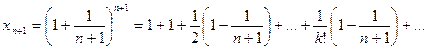
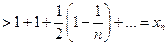 ,
,
т. е. 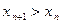 и, следовательно, последовательность
и, следовательно, последовательность 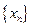 возрастающая.
возрастающая.
Таким образом, установлено, что последовательность 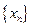 монотонно возрастающая и ограниченна сверху. Следовательно, существует и конечен предел этой последовательности:
монотонно возрастающая и ограниченна сверху. Следовательно, существует и конечен предел этой последовательности: 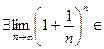 R.
R.
Предел этой последовательности называется числом e. Некоторое количество первых значащих цифр его численного значения приведено выше.
Для их запоминания часто применяют следующее мнемоническое правило: запомните число 2,7; далее два раза напишите год рождения Льва Толстого 1828;
и два раза половина прямого угла 45, между которыми стоит прямой угол 90.
Обозначение 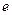 ввел Я. Эйлер (
ввел Я. Эйлер (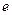 - первая буква в слове exponenta). Обозначение стало общеупотребительным, так как напоминает и об Я. Эйлере (
- первая буква в слове exponenta). Обозначение стало общеупотребительным, так как напоминает и об Я. Эйлере (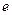 - первая буква фамилии Euler Leonard, 1707-1783).
- первая буква фамилии Euler Leonard, 1707-1783).
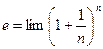 .
.
Эйлер ввел также 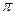 (греч.
(греч. 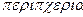 - окружность) в 1736 г. И хотя еще в 1706 г. то же сделал У. Джонсон (W. Johnson), только после Эйлера обозначение стало обще употреби-тельным.
- окружность) в 1736 г. И хотя еще в 1706 г. то же сделал У. Джонсон (W. Johnson), только после Эйлера обозначение стало обще употреби-тельным.
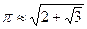 , 3.141…3.146
, 3.141…3.146
Тот же результат можно получить, воспользовавшись неравенством Я. Бернулли:
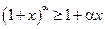 если
если 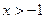 и
и 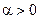 , причем
, причем 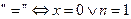 .
.
Для натурального 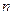 ,
, 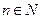 , и положительного
, и положительного 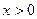 неравенство очевидно из формулы бинома:
неравенство очевидно из формулы бинома:
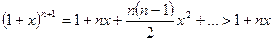 . Для натурального
. Для натурального 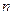 ,
, 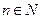 , и
, и 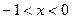 доказывается методом математической индукции: первый шаг индукции
доказывается методом математической индукции: первый шаг индукции 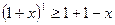 , предположение индукции
, предположение индукции 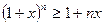 , индуктивный шаг
, индуктивный шаг 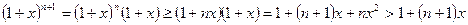 .
.
В общем случае (для вещественных показателей) легко доказывается методами дифференциального исчисления.
Для последующего рассуждения требуется только доказанное здесь (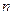 натуральное).
натуральное).
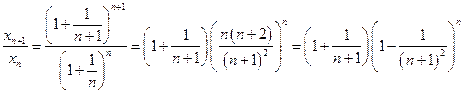 >
>
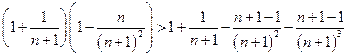 =
=
= 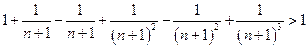 .
.
- последовательность 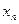 возрастает (
возрастает (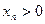 ).
).
Далее определим последовательность:
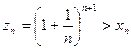 . Тогда для нее:
. Тогда для нее: 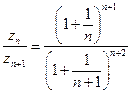 =
= 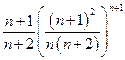 =
=
= 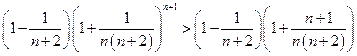 >
>
> 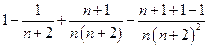 =
= 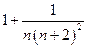 > 1.
> 1.
- последовательность 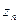 убывает. Очевидно
убывает. Очевидно 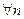
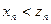 .
.
Если 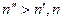 , то
, то 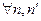
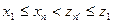 - любой член одной последовательности ограничивает другую последовательность.
- любой член одной последовательности ограничивает другую последовательность.
Следовательно: 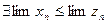 . Но
. Но 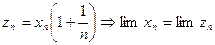 .
.
 2014-02-24
2014-02-24 923
923








