Ряд дляe. Series fore

Отбрасывая в выражении 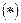для 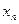все (положительные) слагаемые после k +1 имеем:

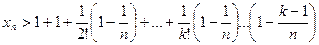
Существование предела слева доказано, предел справа очевидно существует, поэтому в пределе 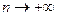получаем двойное неравенство:

; .

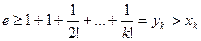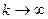Учитывая что, и правая и левая части неравенства стремятся к 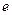, по принципу двустороннего ограничения получаем:

;

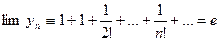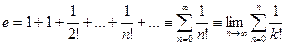
- представление 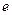в виде суммы числового ряда.

Теперь: = <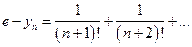

<= …

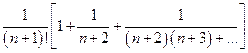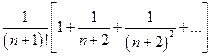Заменяем множители, большие 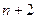на 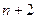(уменьшение знаменателей – увеличение слагаемых и суммы)

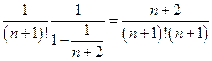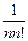… = < , поскольку:

.

Значит 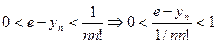. Обозначая 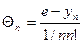, , 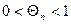получим

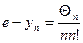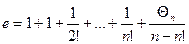. Þ , где .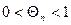

Пользуясь этой формулой легко вычислить 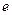вручную (без калькулятора) с любой разумной точностью (достаточной для большинства «практических» задач). Прежде чем делать это, получим ещё одно представление числа 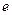в виде. Для этого заметим, что:

=

= =

= .

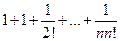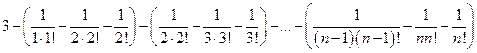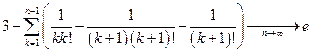Величина убывает к 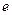, поскольку слагаемые в сумме положительны.

=

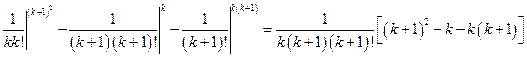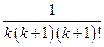= Þ .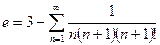

Для разности 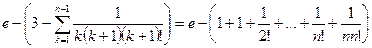имеем

=

= <

< =

= ,

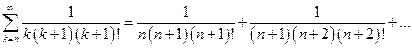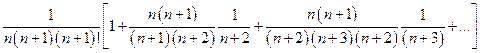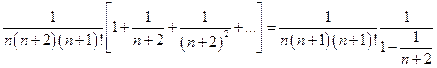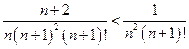поскольку .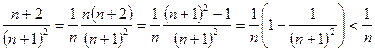

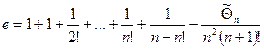, где .

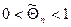Пользуясь полученными формулами, можно вычислим число 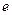с необходимым количеством верных знаков после запятой.