РАЗДЕЛ. Дифференциальное исчисление
Пусть 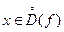 внутренняя точка области определения.
внутренняя точка области определения.
Def. Функция 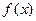 называется дифференцируемой в точке x если:
называется дифференцируемой в точке x если:
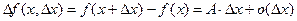 и А не зависит от
и А не зависит от 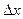 .
.
Если функция дифференцируема, то ее приращение имеет главную часть 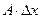 .
.
F°. Если функция дифференцируема, то она непрерывна т.к. при  .
.
(но ….. не наоборот).
Def. Функцию назовем дифференцируемой справа (слева) если:
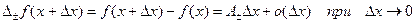 .
.
Здесь 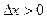 (
(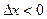 ).
).
Пусть 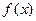 - дифференцируема Þ
- дифференцируема Þ
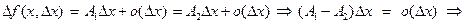
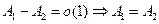 .
.
F°. Если 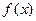 дифференцируема в точке то она дифференцируема справа и слева в этой точке и
дифференцируема в точке то она дифференцируема справа и слева в этой точке и 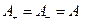 (и наоборот).
(и наоборот).
Пример: Функция 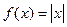 в нуле не дифференцируема.
в нуле не дифференцируема.
Если 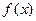 дифференцируема в точке, то в окрестности этой точки ее приращение может быть представлено в виде суммы линейной функции от
дифференцируема в точке, то в окрестности этой точки ее приращение может быть представлено в виде суммы линейной функции от 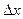 плюс бесконечно малая более высокого порядка, чем
плюс бесконечно малая более высокого порядка, чем 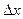 .
.
 2014-02-24
2014-02-24 654
654








