2014-02-24
5989
Решение алгебраических уравнений 1, 2, 3, 4 степени.
I.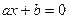 
. 1)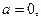 
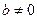– нет решений;
2) 
, 
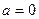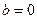– бесконечно много решений;
3) 
, 
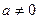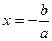– единственное решение.
II.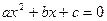 
, () 
.
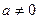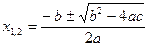III.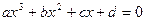 
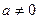, (). Перейдем к приведенному кубическому уравнению:
, и произведем замену неизвесной: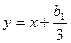 
.
тогда: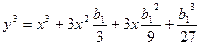 
; 
; 
,
.
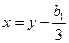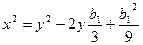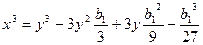Подставляя полученные выражения в уравнение, получим:
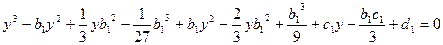Þ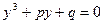 
.
Получается неполное кубическое уравнение, в котором
; 
.
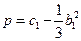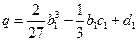Решение получившегося неполного кубического уравнения ищем в виде: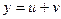 
.
Тогда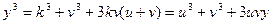 
Þ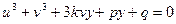 
И, следовательно: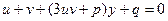 
.
Положив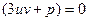 
, получим систему уравнений 
.
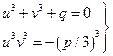т.е.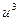 
и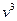 
являются корнями квадратного уравнения 
.
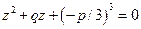Решая это уравнение, найдем
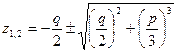Þ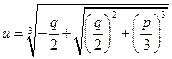 
; 
.
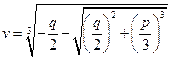Полученные три значении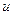 
и три значения 
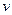не могут суммироваться в произвольных сочетаниях. Они должны удовлетворять соотношению 
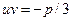. Оказывается, есть ровно три пары 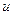и 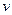, удовлетворяющих этому соотношению.
Отсюда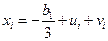 
, 
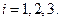Найдены три корня кубического уравнения.
.
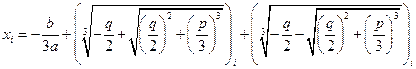Это и есть формулы Кардано для нахождения корней кубического уравнения.
Пример 1. Решить уравнение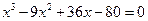 
.
Полагая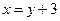 
, получим неполное кубическое уравнение 
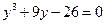. К этому уравнению можно применить формулы Кардано. Здесь 
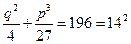, поэтому
|
|
|
.
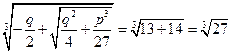Одним из значений этого кубического корня будет число 3. Произведение этого значения на соответствующее ему значение другого кубического корня, входящего в формулу, должно равняться числу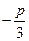 
, т.е. в нашем случае равняться числу (–3). Искомым значением второго корня будет, следовательно, число (–1) и поэтому 
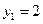. Разделив неполное уравнение на (
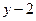), получим квадратное уравнение с корнями 
.
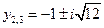Тогда корнями исходного кубического уравнения будут: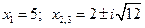
.
Пример 2. Решить уравнение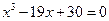 
.
Здесь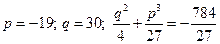 
. Тогда:
.
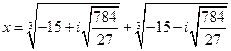Корнями данного кубического уравнения будут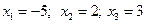 
.
Решение этого уравнения показывает, что далеко не всегда корни кубического уравнения (даже если они вполне благополучные) удается найти так просто, как хотелось бы.
IV. Рассматриваем уравнение четвертой степени:
, 
.
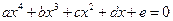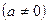Мы приведем решение, полученное Феррари.
Приведенное уравнение имеет вид: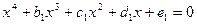 
.
Осуществляя замену переменной: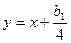 
; 
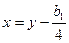, получим неполное уравнение четвертой степени: 
.
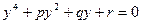Запишем уравнение в виде: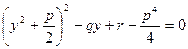 
.
Введем параметр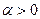 
так, чтобы:
.
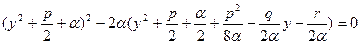Потребуем, чтобы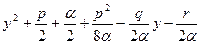 
было полным квадратом, тогда идея
состоит в том, чтобы представить полученное уравнение в виде разности квадратов
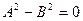, с последующим разложением его в произведение 
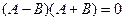и решением получившихся квадратных уравнений.
Для реализации этой идеи дискриминант квадратного уравнения должен быть равен нулю.
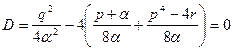. Тогда 
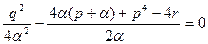Þ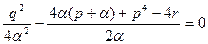
Þ Þ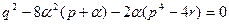 
.
и для нахождения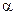 
имеем кубическое уравнение: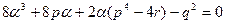 
.
При этом, если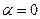 
; 
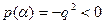и если 
; 
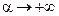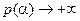
т.е. уравнение обязательно имеет положительный корень.
