РАЗДЕЛ. Неопределенный интеграл
Def. Уравнение которое, кроме неизвестной функции и аргумента, содержат и производные искомой функции конечных порядков, называется обыкновенным дифференциальным уравнением. Причем высший порядок производной входящей в уравнение называется порядком уравнения.
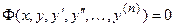 - неявное дифференциальное уравнение n -го порядка.
- неявное дифференциальное уравнение n -го порядка.
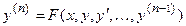 - явное дифференциальное уравнение n -го порядка.
- явное дифференциальное уравнение n -го порядка.
Def. Частным решением дифференциального уравнения на невырожденном промежутке Х, называется любая функция, которая при подстановке в уравнение обращает его в тождество на этом промежутке. Множество всех частных решений дифференциального уравнения называется общим решением дифференциального уравнения.
Рассмотрим явное дифференциальное уравнение первого порядка:
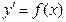
Любое частное решение указанного уравнения называется первообразной функции 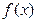 и обозначается
и обозначается 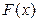 т.е.
т.е. 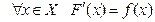 .
.
Example:
1˚. Если 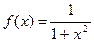 , то
, то 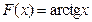 (т.к.
(т.к. 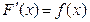 ).
).
2˚. Если 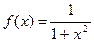 , то
, то 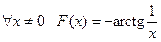 (т.к.
(т.к. 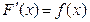 ).
).
Из примеров видно, что одна и та же 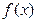 может иметь не одну первообразную.
может иметь не одну первообразную.
Теорема (об общем виде первообразной). Если 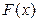 и
и 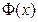 две первообразные одной функции
две первообразные одной функции 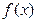 , то
, то 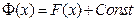 .
.
Δ 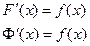
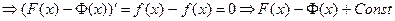 ▲.
▲.
F˚. Первообразная функции на промежутке является первообразной этой же функции на любом невырожденном подпромежутке.
Def. Общее решение дифференциального уравнения 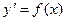 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 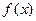 (обозначается
(обозначается 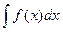 )
)
При этом: 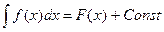
Связь неопределенного интегрирования и дифференцирования:
1˚. 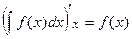 ; 2˚.
; 2˚. 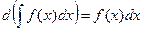 ; 3˚.
; 3˚. 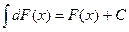 .
.
Линейность неопределенного интеграла:
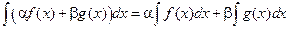 ,
, 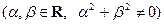 .
.
 2014-02-24
2014-02-24 528
528








