Схема Горнера. Возвратные уравнения.
Многочлены. Теорема Безу и ее следствия. Рациональные корни уравнений.
4.
Алгебраическим полиномом степени 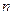 называется конструкция вида:
называется конструкция вида:
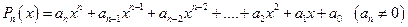 .
.
Пусть заданы алгебраические полиномы: 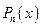 и
и 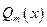 , причем
, причем 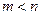 . Тогда существуют два других полинома – один
. Тогда существуют два других полинома – один 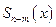 степени
степени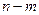 , другой
, другой 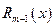 – степени, не превышающей числа
– степени, не превышающей числа 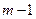 , такие что
, такие что 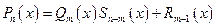 . Полином
. Полином 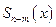 называется неполным частным от деления полинома
называется неполным частным от деления полинома 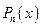 на полином
на полином 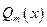 , а полином
, а полином 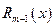 остатком от такого деления. Если, при этом,
остатком от такого деления. Если, при этом, 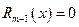 то говорят, что полином
то говорят, что полином 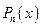 делится на полином
делится на полином 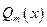 без остатка, а полином
без остатка, а полином 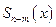 называется полным частным, или просто частным от деления полинома
называется полным частным, или просто частным от деления полинома 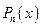 на полином
на полином 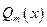 .
.
В случае 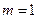 приведенная формула имеет вид
приведенная формула имеет вид
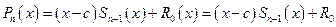 .
.
Т°. (Безу) Остаток от деления полинома 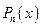 на двучлен
на двучлен 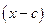 равен значению полинома
равен значению полинома 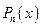 в точке
в точке 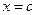 , т.е.
, т.е. 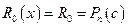 .
.
Т°. (следствие из т° Безу) Полином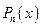 делится на двучлен
делится на двучлен 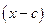 тогда и только тогда когда
тогда и только тогда когда 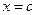 является корнем полинома
является корнем полинома 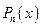 .
.
Т°. (следствие из т° Безу) Если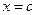 является корнем полинома
является корнем полинома 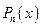 , т.е.
, т.е. 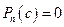 то
то
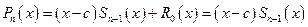 .
.
Это следствие из теоремы Безу позволяет многочлен с известными (полностью или частично) корнями разложить на множители.
Т°. Если алгебраическое уравнение 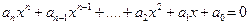 имеет целые коэффициенты
имеет целые коэффициенты 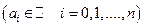 и рациональное число
и рациональное число 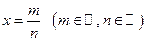 является его корнем, то число
является его корнем, то число 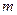 является делителем свободного члена уравнения, а число
является делителем свободного члена уравнения, а число 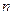 является делителем старшего коэффициента уравнения.
является делителем старшего коэффициента уравнения.
Это утверждение позволяет из всего множества рациональных чисел сразу отобрать только те, которые могут быть корнями уравнения. Установить, являются ли они корнями уравнения можно непосредственной подстановкой. При этом, удобно значение полинома в точке вычислить способом, который предложенным Горнером. Проиллюстрируем схему Горнера на конкретном примере (это верно передает суть метода и не загромождает выкладку).
Полином 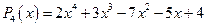 запишем в виде, предложенном Горнером:
запишем в виде, предложенном Горнером:
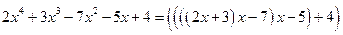 .
.
Запись, стоящая справа позволяет вычислить значение полинома 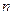 -й степени в точке не более чем за
-й степени в точке не более чем за 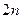 операций. Оказывается это самый экономичный способ вычисления значения полинома в точке. На основе такой записи полинома можно построить вычислительную табличку, которая, зачастую, также называется схемой Горнера.
операций. Оказывается это самый экономичный способ вычисления значения полинома в точке. На основе такой записи полинома можно построить вычислительную табличку, которая, зачастую, также называется схемой Горнера.
В верхней строке таблицы (кроме первой клетки) записываются коэффициенты исходного полинома в порядке убывания степеней. В первой клетке нижней строки таблицы записывается значение аргумента, при котором вычисляется значение полинома. Остальные клетки нижней строки заполним по формулам:
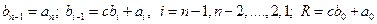 .
.
| – | an | an- 1 | an- 2 | … … | a 2 | a 1 | a 0 |
| c | bn- 1 | bn- 2 | bn- 3 | … … | b 1 | b 0 | R |
Заполнив табличку, отметим что в последней клетке нижней строки стоит 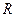 – значение полинома в точке
– значение полинома в точке 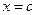 . В клетках нижней строки, кроме первой и последней, стоят коэффициенты частного от деления исходного полинома на двучлен
. В клетках нижней строки, кроме первой и последней, стоят коэффициенты частного от деления исходного полинома на двучлен 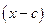 .
.
Для полинома 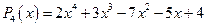 и
и 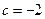 вычисляя значение полинома в точке
вычисляя значение полинома в точке 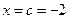 получаем:
получаем:
| -7 | -5 | ||||
| -2 | -1 | -5 | -6 |
Т. е. установлено что 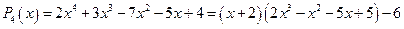 .
.
Задачи для решения:1*, 2*, …, 21*
Решить алгебраические уравнения:
1*. 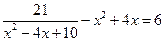 ; 2*.
; 2*. 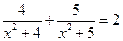 ;
;
3*. 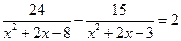 ; 4*.
; 4*. 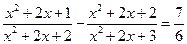 ;
;
5*. 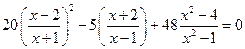 ;
;
6*. Найти сумму коэффициентов многочлена:
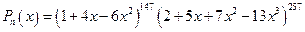 .
.
7*. Делится ли многочлен 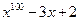 на
на 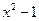 ?
?
8*. Найти остаток от деления 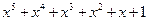 на
на 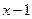 .
.
9*. Некоторый многочлен при делении на 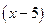 дает в остатке 5, а при делении на
дает в остатке 5, а при делении на 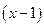 дает в остатке 3. Найти остаток от деления того же многочлена на
дает в остатке 3. Найти остаток от деления того же многочлена на 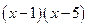 .
.
10*. Остаток от деления 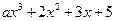 на
на 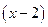 равен 35, а от деления на
равен 35, а от деления на 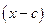 остаток равен 320. Найти а и с.
остаток равен 320. Найти а и с.
С помощью схемы Горнера решить следующие уравнения:
11*. 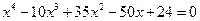 ,
,
12*. 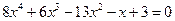 ,
,
13*. 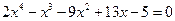 ,
,
14*. 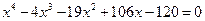 .
.
Решить возвратные уравнения:
15*. 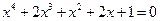 ,
,
16*. 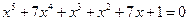 ,
,
17*. 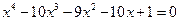 ,
,
18*. 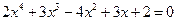 .
.
19*. Решить следующие уравнения разложив левую часть в произведение двух квадратных трехчленов:
а) 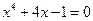 , б)
, б) 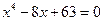 .
.
20*. Найти а при которых уравнение 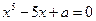 имеет два совпадающих корня.
имеет два совпадающих корня.
21*. Число 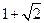 является корнем уравнения
является корнем уравнения
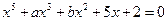 .
.
Найти остальные корни, зная что а и b рациональные числа.
 2014-02-24
2014-02-24 956
956








